filmov
tv
The mystery of 0.577 - Numberphile

Показать описание
The harmonic series and the elusive Euler–Mascheroni constant.
More links & stuff in full description below ↓↓↓
Featuring Dr Tony Padilla.
NUMBERPHILE
Videos by Brady Haran
More links & stuff in full description below ↓↓↓
Featuring Dr Tony Padilla.
NUMBERPHILE
Videos by Brady Haran
The mystery of 0.577 - Numberphile
Cicada 3301: An Internet Mystery
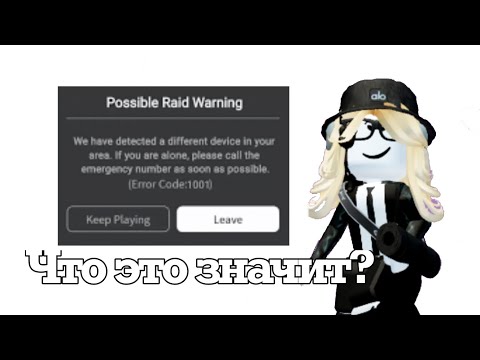
Что значат разные ошибки в роблоксе и что делать? Ошибка 1001 самая страшная...
SCP - 031 | Part 2 'NORTH KOREA HOTEL'☢️ #scp #scpfoundation #viral #shortsvideo #animatio...
THE MYSTERY OF 0 NUMBER // AZ MOVIE WORLD // TEASER ----
Dark Riddle 18.2.0: Hello Neighbor, Game in mystery car spy, New House, New Skin: Part 577
This is the Right Response to the LGBT Issue
Naruto Uzumaki, Sakura haruno, Sasuke Uchiha Evolution #sakamachi
Bewakoofi ki bhi haad hoti hai #littleglove #funnybahu #shorts aadya 😢
🌟Mystery smashies unboxing #trending #hellokitty #fun #pompompurin #viral #shorts #asmr #viralshort...
Hit The Target, Win $300,000
Mystery of 4,000 year old ancient human portrait #facts #historicalplay #history
Annabelle: The Real Haunted Doll #shorts #scary #horror #facts #paranormal #mystery #viral #ghosts
Please Subscribe to my channel❤️ #shorts #youtubeshorts #shortsfeed #roadto1ka.
It’s a mystery 🤷♀️ #texasprisons #criminaljustice #parole #meme #prisonmeme
True story #conspiracy #mystery #truecrime #crime #shorts #short
Handmade Hero Day 577 - Adding Octahedral Light Atlases
THE MEMORARE / 'Remember, O Most Gracious Virgin Mary...'
#CivilWar Gold? A #history mystery... #didyouknow #1800s
Wendy and Eric Help and Learn about Sea Animals
Luffy Discovers New Haki! | One Piece
CREEPIEST ERRORS on ROBLOX
Techno Gamerz Call Me 📱 Whatsapp Call With Techno Gamerz 😱 Techno Gamerz Video Call #shorts
disturbing mysteries that were solved 4
Комментарии
 0:10:03
0:10:03
 0:17:54
0:17:54
 0:02:24
0:02:24
 0:01:01
0:01:01
 0:00:30
0:00:30
 0:08:37
0:08:37
 0:00:51
0:00:51
 0:00:15
0:00:15
 0:00:22
0:00:22
 0:00:17
0:00:17
 0:13:17
0:13:17
 0:00:56
0:00:56
 0:00:30
0:00:30
 0:00:15
0:00:15
 0:00:10
0:00:10
 0:00:57
0:00:57
 2:24:21
2:24:21
 0:01:01
0:01:01
 0:00:43
0:00:43
 0:03:00
0:03:00
 0:01:40
0:01:40
 0:08:11
0:08:11
 0:00:27
0:00:27
 0:21:53
0:21:53