filmov
tv
2 different exponential equations
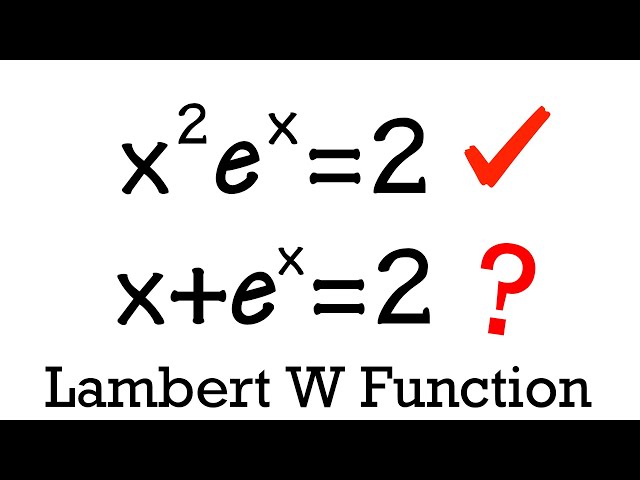
Показать описание
We will solve 2 different exponential equations: x^2*e^x=2 and x+e^x=2 by using the Lambert W function.
Solving equations with Lambert W functions,
blackpenredpen
Solving equations with Lambert W functions,
blackpenredpen
2 different exponential equations
how to solve an exponential equation with two different bases
How to solve an exponential equation with two different bases
How do I find x? Exponential equation with two different bases. Reddit precalculus r/Homworkhelp
How to solve an exponential equation with two different bases
Learn How to Solve Exponential Equations Using Two Different Methods | Step-by-Step Tutorial
Solving an exponential equation with different bases
Solving exponential equations with different bases
A Nice Exponential Equation | Can you solve this? | Algebra Simplification Problem
Solving Exponential Equation with Different Bases
Solving Exponential Equations
How to Solve 2^(x - 2) = 3^(2x - 4) Exponential Equation with Different Base with Logarithms
Solving Exponential Equation
solving a quadratic exponential equation with different bases
Exponential Equations - Algebra and Precalculus
Solving exponential equation with logarithm | Logarithms | Algebra II | Khan Academy
Solving Simultaneous With Exponential directly.
Can you solve this? | Exponential Equation | Algebra Problem.
How to Solve Exponential Equations using Logarithms - No Common Base Present
Solving exponential equation | Exponential and logarithmic functions | Algebra II | Khan Academy
Solving Exponential and Logarithmic Equations
LAWS OF EXPONENTS | MATHS TRICKS
Exponential Equation Given a Table
Simultaneous Exponential Equations
Комментарии
 0:09:19
0:09:19
 0:03:21
0:03:21
 0:05:11
0:05:11
 0:07:47
0:07:47
 0:05:50
0:05:50
 0:12:15
0:12:15
 0:03:01
0:03:01
 0:04:41
0:04:41
 0:06:06
0:06:06
 0:04:10
0:04:10
 0:16:36
0:16:36
 0:05:06
0:05:06
 0:00:56
0:00:56
 0:06:52
0:06:52
 0:05:58
0:05:58
 0:02:51
0:02:51
 0:13:50
0:13:50
 0:03:33
0:03:33
 0:05:47
0:05:47
 0:05:12
0:05:12
 0:07:08
0:07:08
 0:00:42
0:00:42
 0:01:32
0:01:32
 0:05:31
0:05:31