filmov
tv
how to solve an exponential equation with two different bases
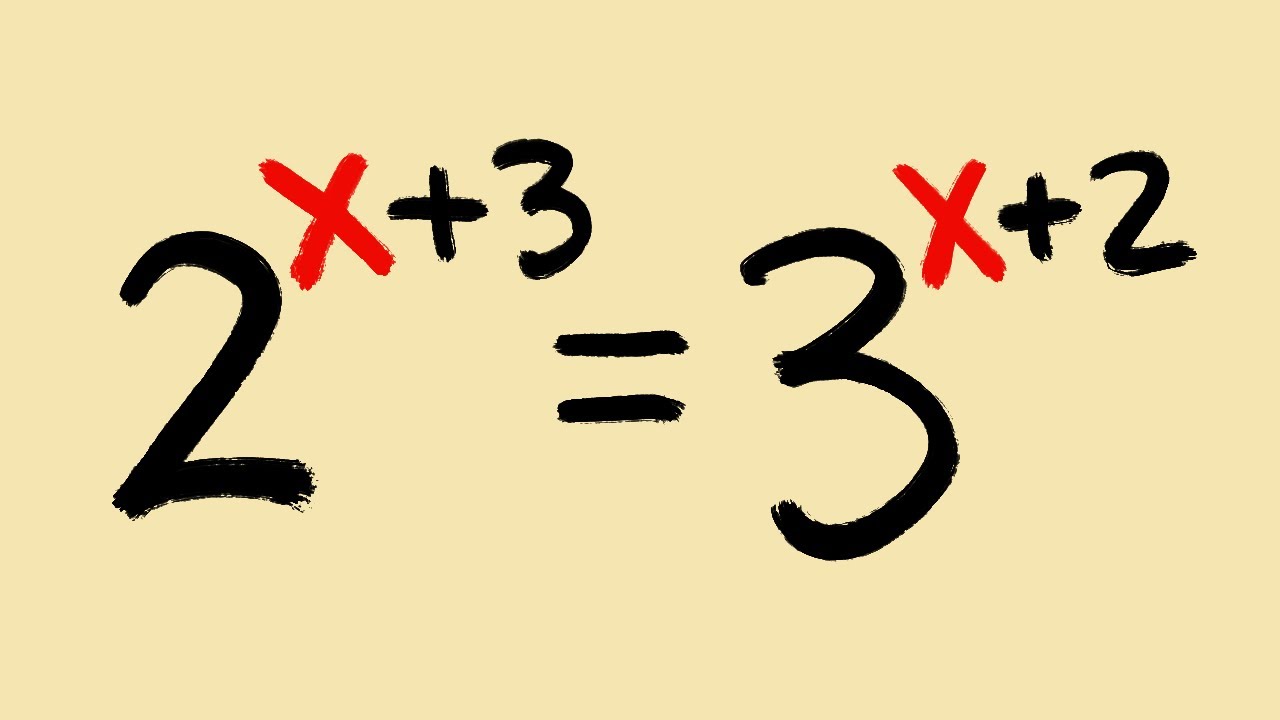
Показать описание
We will solve the exponential equation 2^(x+3)=3^(x+2) which has two different bases. This is a must-know algebra problem with exponents and logarithms. For more algebra tutorials, please subscribe to @bprpmathbasics
Use "WELCOME10" for 10% off
-----------------------------
"Just Algebra" (by blackpenredpen) is dedicated to helping middle school, high school, and community college students who need to learn algebra. Topics include how to solve various equations (linear equations, quadratic equations, square root equations, rational equations, exponential equations, logarithmic equations, and more), factoring techniques, word problems, functions, graphs, Pythagorean Theorem, and more. We will also cover standardized test problems such as the SAT. Feel free to leave your questions in the comment!
-----------------------------
#justalgebra
Use "WELCOME10" for 10% off
-----------------------------
"Just Algebra" (by blackpenredpen) is dedicated to helping middle school, high school, and community college students who need to learn algebra. Topics include how to solve various equations (linear equations, quadratic equations, square root equations, rational equations, exponential equations, logarithmic equations, and more), factoring techniques, word problems, functions, graphs, Pythagorean Theorem, and more. We will also cover standardized test problems such as the SAT. Feel free to leave your questions in the comment!
-----------------------------
#justalgebra
Solving Exponential Equations
How do you solve an exponential equation with e as the base
Classwiz How-To: Solving an Exponential Equation
Exponential Equations - Algebra and Precalculus
Solving Exponential Equations
how to solve an exponential equation with two different bases
Solve an exponential equation by taking log of both sides & approximating the value
How to solve an exponential equation with two different bases
A Beautiful Exponential Equation | Can You Solve This?
Solving exponential equations with different bases
Solving Exponential Equation
Solving Exponential Equations | How to Solve Exponential Equations | General Mathematics
How to solve an exponential equation with two different bases
Solving an exponential equation
Solving Exponential and Logarithmic Equations
What is an Exponent? | An Intro to Exponents | Math with Mr. J
Using the change of base to help solve an exponential equation
Solving Simultaneous With Exponential directly.
Solving an exponential equation with different bases
Solving Exponential Equation
Solving Exponential Equations Using Logarithms & The Quadratic Formula
Exponential Equation Grade 10
Learn How to Solve Exponential Equations Using Two Different Methods | Step-by-Step Tutorial
Solving exponential equations by using the natural log
Комментарии
 0:16:36
0:16:36
 0:02:47
0:02:47
 0:01:14
0:01:14
 0:05:58
0:05:58
 0:01:46
0:01:46
 0:03:21
0:03:21
 0:03:23
0:03:23
 0:05:11
0:05:11
 0:09:01
0:09:01
 0:04:41
0:04:41
 0:00:56
0:00:56
 0:11:33
0:11:33
 0:05:50
0:05:50
 0:03:14
0:03:14
 0:07:08
0:07:08
 0:07:21
0:07:21
 0:04:22
0:04:22
 0:13:50
0:13:50
 0:03:01
0:03:01
 0:02:56
0:02:56
 0:11:05
0:11:05
 0:01:39
0:01:39
 0:12:15
0:12:15
 0:02:23
0:02:23