filmov
tv
How do I find x? Exponential equation with two different bases. Reddit precalculus r/Homworkhelp
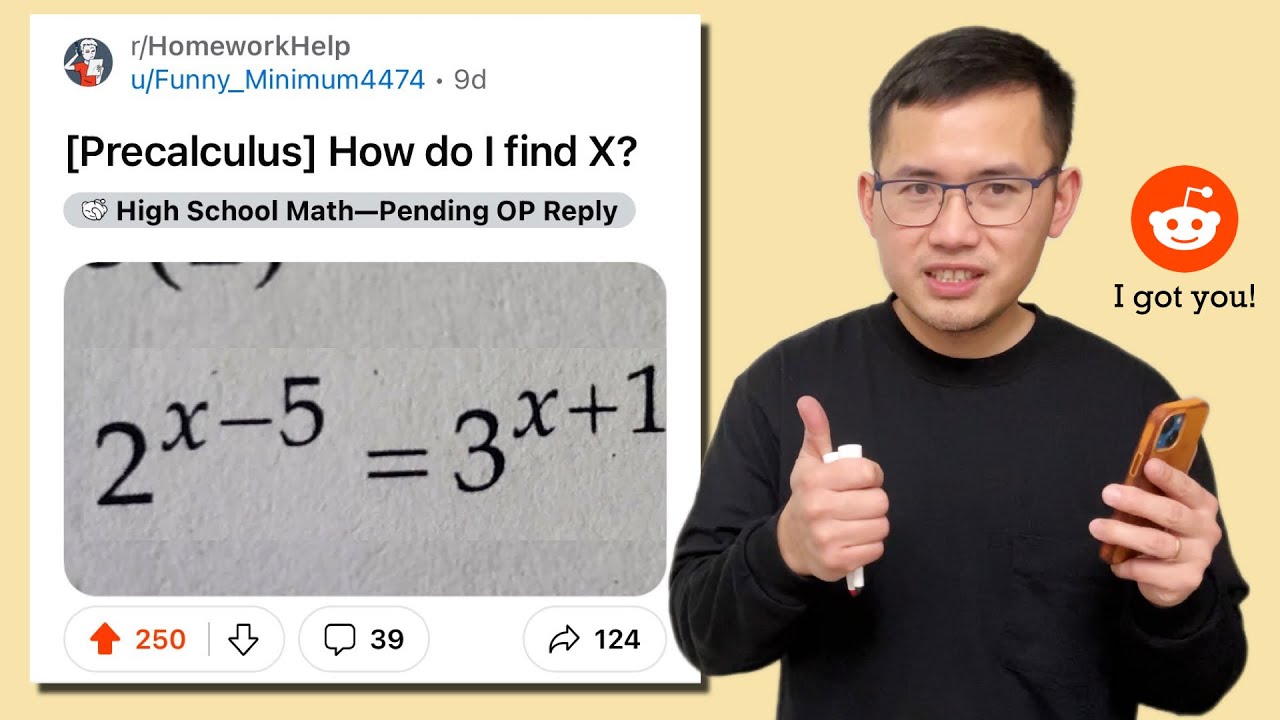
Показать описание
-----------------------------
-----------------------------
#math #algebra #mathbasics
How do I find x? Exponential equation with two different bases. Reddit precalculus r/Homworkhelp
How to find the x and y intercept from an equation
How To Find The X and Y Intercepts of a Line
How do find the x and y intercepts and graph
How to Find X and Y Intercepts of a Function Explained!
iPhone X: How to Use Siri (3 Ways) Step by Step
How to find the domain of the square root function M(x)=sqrt(1+1/x)
How Do You Find x In Vertical Angles?
How to Find the X and Y Intercept of a Line ( Example 1 ) Intermediate Algebra , Lesson 60
How To Find X and Y with Parallel Angles -Alternate Interior Angles and Supplementary
How to find the x-intercept, y-intercept, and slope of a line. (algebra bascis)
#18. How to Find the Function Compositions: (f o g)(x), (g o f)(x), (f o g)(2), and (g o f)(2)
How to Get the X Intercept From MX+B
How To Find The X and Y Intercepts of a Rational Function | Algebra 2
How to Find X or Y With Fitted Curve
(fog)(x) and (gof)(x): How to find them, given f(x) and g(x).
How do you find the x and y intercept of a quadratic
How to Set X and Y Axis in Excel
Calculate angle X in a 5-sided irregular Polygon | Learn how to Solve this Geometry problem Quickly
Learn how to find the solutions x intercepts and vertex of a quadratic in vertex form ex 7
How To Get X Profile Link (Twitter) - Full Guide
How to find the x and y intercepts of a graph table and equation
How To Solve Exponential Equation x^5=9^x || Solving Exponential Equations.
How to solve equations with x in the numerator
Комментарии
 0:07:47
0:07:47
 0:03:32
0:03:32
 0:13:08
0:13:08
 0:04:55
0:04:55
 0:08:28
0:08:28
 0:03:50
0:03:50
 0:04:56
0:04:56
 0:04:45
0:04:45
 0:05:40
0:05:40
 0:05:00
0:05:00
 0:03:14
0:03:14
 0:03:38
0:03:38
 0:01:27
0:01:27
 0:08:35
0:08:35
 0:00:55
0:00:55
 0:02:41
0:02:41
 0:07:08
0:07:08
 0:00:39
0:00:39
 0:03:17
0:03:17
 0:03:04
0:03:04
 0:01:53
0:01:53
 0:07:02
0:07:02
 0:11:56
0:11:56
 0:01:49
0:01:49