filmov
tv
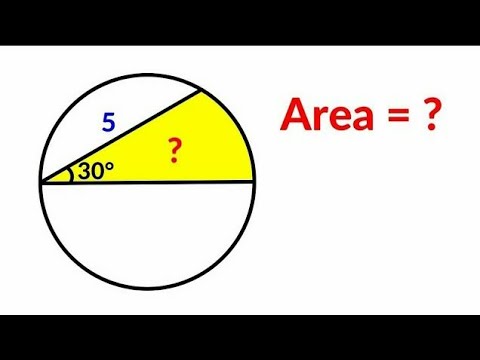
A nice geometry problem from New Zealand

Показать описание
🌟Support the channel🌟
🌟my other channels🌟
🌟My Links🌟
🌟How I make Thumbnails🌟
🌟Suggest a problem🌟
🌟my other channels🌟
🌟My Links🌟
🌟How I make Thumbnails🌟
🌟Suggest a problem🌟
Olympiad Mathematics | A Very Nice Geometry Problem
Math Olympiad | A Very Nice Geometry Problem
A nice geometry problem from New Zealand
Olympiad Mathematics | A Very Nice Geometry Problem
a nice geometry problem in the complex plane.
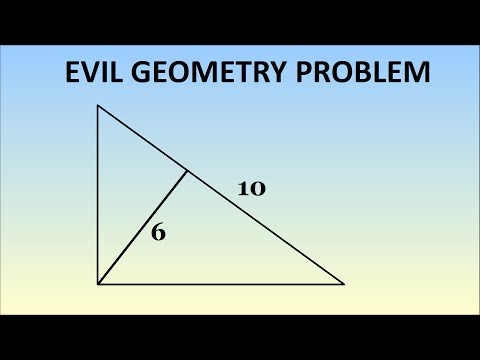
Evil Geometry Problem
A beautiful and challenging geometry construction
A simple geometry problem with a nice generalization.
China | Can You Solve this ? | Math Olympiad 👇
A nice quick geometry problem.
Angle Chasing Problem - Moscow 1952 | A Nice Geometry Challenge
A nice geometry problem with complex numbers.
A nice geometry trick!
A nice Iranian geometry problem
How to prepare your Geometry for the IMO and other math competitions
Challenging Math Olympiad Problem | Geometry Question | Mathematics | 2 Methods
Can You Find Angle X? | Geometry Challenge!
I have a difficult geometry problem where I need to find angle x.
A quick geometry problem.
The hardest 'easy' geometry problem.
A quick geometry problem.
Incredibly hard geometry problem from Russia
The Three Square Geometry Problem - Numberphile
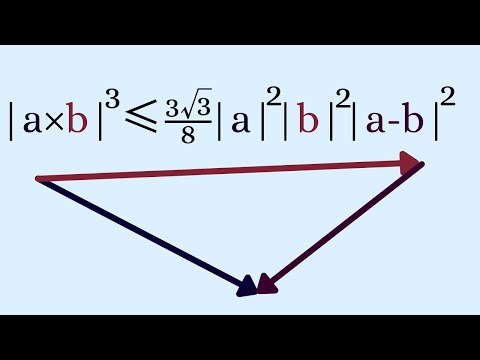
a nice mix of geometry and calculus, using vectors.
Комментарии
 0:11:17
0:11:17
 0:12:38
0:12:38
 0:06:36
0:06:36
 0:11:21
0:11:21
 0:09:23
0:09:23
 0:03:23
0:03:23
 0:04:49
0:04:49
 0:13:11
0:13:11
 0:14:22
0:14:22
 0:04:58
0:04:58
 0:09:25
0:09:25
 0:11:39
0:11:39
 0:12:30
0:12:30
 0:05:34
0:05:34
 0:05:42
0:05:42
 0:25:44
0:25:44
 0:08:44
0:08:44
 0:07:33
0:07:33
 0:05:49
0:05:49
 0:16:40
0:16:40
 0:08:22
0:08:22
 0:09:27
0:09:27
 0:12:21
0:12:21
 0:11:43
0:11:43