filmov
tv
Olympiad Mathematics | A Very Nice Geometry Problem
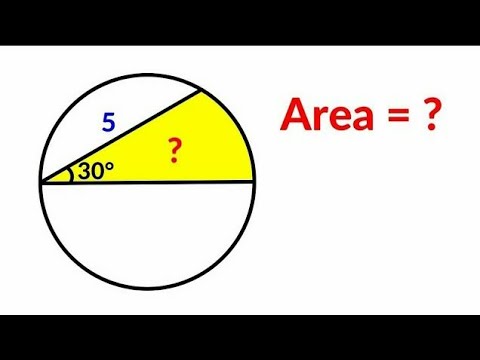
Показать описание
Olympiad Mathematics | A Very Nice Geometry Problem
Math Olympiad | A Very Nice Geometry Problem | 2 Different Methods
Math Olympiad | A Very Nice Geometry Problem
A beautiful international math olympiad problem
A Nice Olympiad Exponential Multiplication Problem #short #olympiad #mathematics #maths #exponents
Math Olympiad Question | Equation solving | You should learn this trick to pass the exam
Norway Math Olympiad Question | You should be able to solve this!
A Nice Math Olympiad Exponential Equation 3^x = X^9
China | Can You Solve this ? | Math Olympiad 👇
Luxembourg - Math Olympiad Question | You should know this trick
Math Olympiad | A Very Nice Geometry Problem | 2 Methods
Olympiad Mathematics | A Very Nice Algebra Problem
Math Olympiad | A Very Nice Geometry Problem
Math Olympiad Practice
A Very Nice Math Olympiad Problem | Solve for x | Algebra
Russian Math Olympiad | A Very Nice Geometry Problem
Russian Math Olympiad Problem | A Very Nice Geometry Challenge | 2 Different Methods
Poland Math Olympiad | A Very Nice Geometry Problem | 2 Different Methods
Canada Math Olympiad Problem | A Very Nice Geometry Challenge
Mexico - A Nice Math Olympiad Exponential Problem
Thailand | Math Olympiad Question | Nice Algebra Equation
Math Olympiad 3^m–2^m=65 | Math Olympiad Problems | Algebra
Math Olympiad | A Very Nice Algebra Problem
Math Olympiad Question | You should know how to solve this!!
Комментарии
 0:13:04
0:13:04
 0:12:38
0:12:38
 0:01:00
0:01:00
 0:00:52
0:00:52
 0:01:54
0:01:54
 0:03:21
0:03:21
 0:02:34
0:02:34
 0:14:22
0:14:22
 0:02:51
0:02:51
 0:13:46
0:13:46
 0:09:15
0:09:15
 0:11:45
0:11:45
 0:01:00
0:01:00
 0:16:04
0:16:04
 0:14:34
0:14:34
 0:27:41
0:27:41
 0:17:18
0:17:18
 0:15:38
0:15:38
 0:08:36
0:08:36
 0:01:26
0:01:26
 0:10:49
0:10:49
 0:08:38
0:08:38
 0:02:24
0:02:24