filmov
tv
a nice geometry problem in the complex plane.

Показать описание
If you are going to use an ad-blocker, considering using brave and tipping me BAT!
Books I like:
Abstract Algebra:
Differential Forms:
Number Theory:
Analysis:
Calculus:
My Filming Equipment:
Japanese Math Olympiad | A Very Nice Geometry Problem
Sweden Math Olympiad | A Very Nice Geometry Problem
a nice geometry problem in the complex plane.
Olympiad Mathematics | A Very Nice Geometry Problem
A Very Nice Geometry Problem | You should be able to solve this!
Math Olympiad | A Very Nice Geometry Problem
Evil Geometry Problem
A Very Nice Geometry Problem | 2 Different Methods !! @learncommunolizer
A Nice Math Olympiad Exponential Problem|singapore math
A simple geometry problem with a nice generalization.
A nice quick geometry problem.
Nice Geometry Problem
A beautiful and challenging geometry construction
Can You Find Angle X? | Geometry Challenge!
Find the distance of the line segment AB | Nice Geometry problem!
A nice geometry trick!
A nice geometry problem with complex numbers.
Challenging Math Olympiad Problem | Geometry Question | Mathematics | 2 Methods
How to prepare your Geometry for the IMO and other math competitions
Find the radius of the circle | A Nice Geometry Problem | Maths Olympiad
A quick geometry problem.
why I think geometry is HARD
A nice Iranian geometry problem
A quick geometry problem.
Комментарии
 0:09:58
0:09:58
 0:08:05
0:08:05
 0:09:23
0:09:23
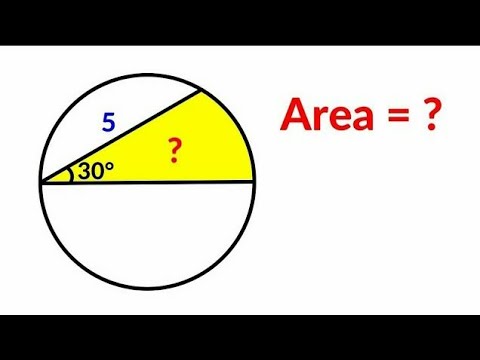 0:11:17
0:11:17
 0:09:24
0:09:24
 0:12:38
0:12:38
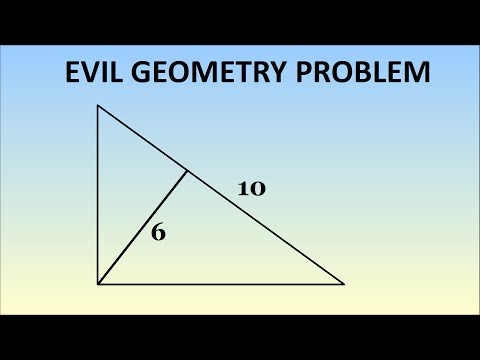 0:03:23
0:03:23
 0:11:01
0:11:01
 0:03:06
0:03:06
 0:13:11
0:13:11
 0:04:58
0:04:58
 0:08:01
0:08:01
 0:04:49
0:04:49
 0:08:44
0:08:44
 0:08:58
0:08:58
 0:12:30
0:12:30
 0:11:39
0:11:39
 0:25:44
0:25:44
 0:05:42
0:05:42
 0:08:02
0:08:02
 0:05:49
0:05:49
 0:06:11
0:06:11
 0:05:34
0:05:34
 0:08:22
0:08:22