filmov
tv
Angle Chasing Problem - Moscow 1952 | A Nice Geometry Challenge

Показать описание
Angle Chasing Problem - Moscow 1952 | A Nice Geometry Challenge
Join this channel to get access to perks:
MEMBERS OF THIS CHANNEL
••••••••••••••••••••••••••••••••••••••••
Mr. Gnome
Sambasivam Sathyamoorthy
ஆத்தங்கரை சண்முகம்
Εκπαιδευτήρια Καντά
AR Knowledge
堤修一
Sidnei Medeiros Vicente
Mark Ludington
Saunak Swar
Join this channel to get access to perks:
MEMBERS OF THIS CHANNEL
••••••••••••••••••••••••••••••••••••••••
Mr. Gnome
Sambasivam Sathyamoorthy
ஆத்தங்கரை சண்முகம்
Εκπαιδευτήρια Καντά
AR Knowledge
堤修一
Sidnei Medeiros Vicente
Mark Ludington
Saunak Swar
Angle Chasing Problem - Moscow 1952 | A Nice Geometry Challenge
Angle Chasing Problem | Find the angle θ | Geometry | Ukrainian Junior Maths Olympiad
A Very Nice Angle Chasing Geometry Problem | Math Olympiad
An example of angle chasing
Find the angle X | Angle Chasing Geometry Problem | Important Geometry Skills Explained
Geometry Angle chasing problem
Angle Chasing - Mastering AMC 10/12
Angle Chasing #1 (Circumcenter)
Chinese Junior Math Olympiad Problem | Angle Chasing Geometry Problem
AMC 8 Math Class 10 - Length of Complex Shapes, Angle Chasing
MOST TRICKY || ANGLE CHASING PROBLEM || geometry
Pembahasan Soal OSN K Matematika SMA 2023 #19 Angle Chasing
Angle Chasing Observation | Geometry | Mathematics Olympiad IOQM 2023 | Abhay Sir | VOS
Can you find the angle | Angle Chasing | Geometry | Quantitative Aptitude
Angle Chasing: Geometry in AMC 8 Class 1
Angle chasing with parallel lines
Geometry : Angle Chasing By PJ Sir
Olympiad Geometry Problem #90: Incircle, Midpoint, Equal Angles
Don't make eye contact
which side are you on? 🇮🇱/🇵🇸 #israel #freepalestine #idf #shortsvideo
Angle Chasing Problems | IOQM Crash Course | JEE Math Rankers | Prashant Jain
Israeli Army 🏅🪬 #bralcon
LIVESTREAM GEO #3B: An absurdly complicated angle chase!
Geometry | Angle Chasing | Three Equilateral Triangle |Mathematical Olympiads | CAT | GMAT #triangle
Комментарии
 0:09:25
0:09:25
 0:06:35
0:06:35
 0:09:41
0:09:41
 0:05:16
0:05:16
 0:08:55
0:08:55
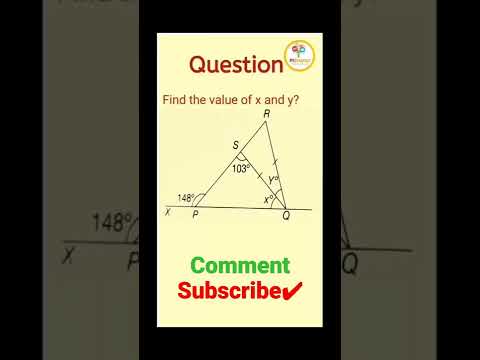 0:00:02
0:00:02
 0:20:48
0:20:48
 0:09:06
0:09:06
 0:04:39
0:04:39
 0:58:03
0:58:03
 0:02:26
0:02:26
 0:01:42
0:01:42
 1:26:11
1:26:11
 0:04:35
0:04:35
 1:13:55
1:13:55
 0:10:20
0:10:20
 0:51:03
0:51:03
 0:08:40
0:08:40
 0:00:05
0:00:05
 0:00:07
0:00:07
 1:27:17
1:27:17
 0:00:19
0:00:19
 1:07:30
1:07:30
 0:05:40
0:05:40