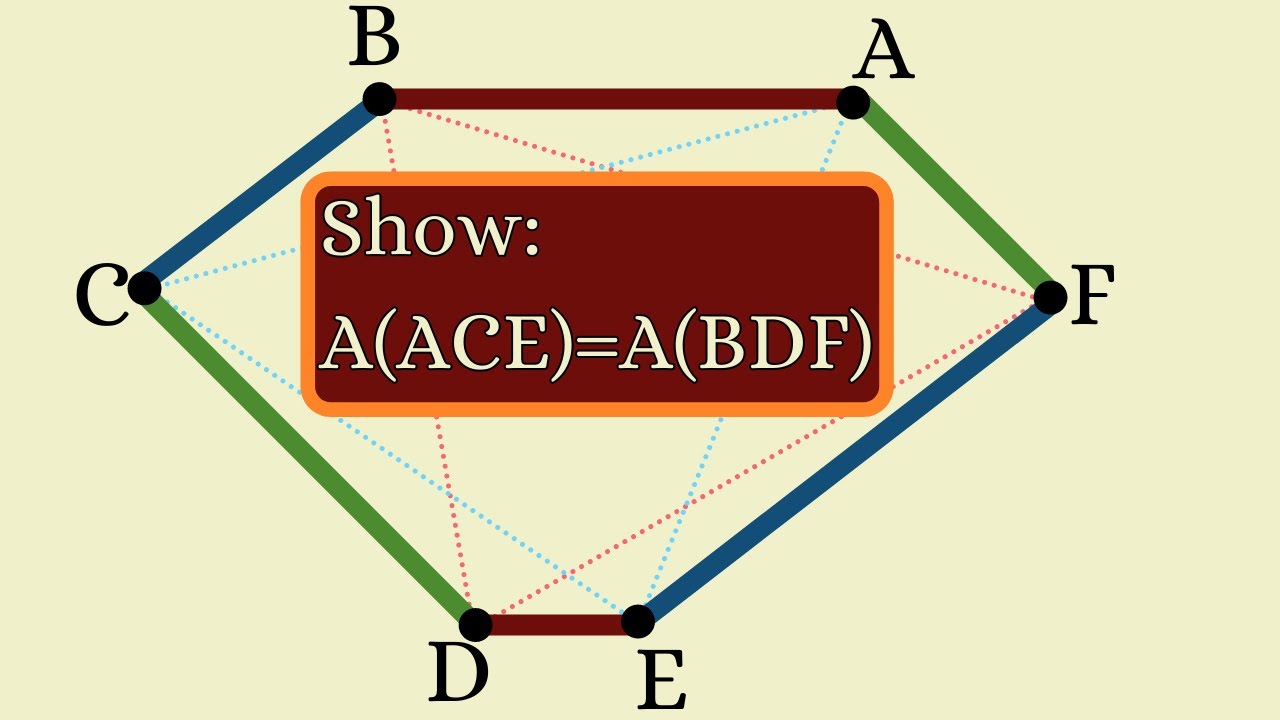
A nice geometry trick!

We use the notion of signed area to solve a geometry problem from a Hungarian contest.

If you are going to use an ad-blocker, considering using brave and tipping me BAT!

Books I like:

Abstract Algebra:

Differential Forms:

Number Theory:

Analysis:

Calculus:

My Filming Equipment:

[Natesrate]

On one of this guys older videos I said the biggest issue in the education system is that most teachers do what he did in that video, this video make's me want to make myself a little more clear. This was not an insult to him, in the video I commented on he was not teaching, he was lecturing by just telling you what he did to find the answer like reading a script, to learn you need to be shown how every step was achieved and then practice yourself to improve on what you've learned. In this video he had more of a teaching style while in the other he was just laying on you "Problem fact fact fact fact solution bye". Teaching is a tool for people new to a topic while lecturing is a discussion to other people who have already been taught the material, I was not criticizing him I was criticizing the education system, teachers just assume kids now a days are going home to actually study what they were taught rather than be on their phones and play games 70% of the time, plus not every child will be interested in ALL the topics being taught to them, that's just not fair, especially when you're being lectured at in an environment dedicated to your learning process.

[GeorgeFoot]

Let P be the intersection of AD and BE. Note as in the video area ABD=ABE; subtract ABP from each to get BDP=APE.
Similarly define Q as the intersection of AD and CF and show that DFQ=ACQ; and define R as the intersection of BE with CF, and show BRF=CER.
Now add these equations together, and also add PQR to each side, to get And the left hand side is clearly BDF while the right hand side is ACE.

[kultek]

Very nice use of the concept of signed area outside of calculus and a very lovely proof.

[yoav]

great video! you can also show this by vectors.the area of atriangle is the cross product of the teo sides of the triangle/2

[AmooBaktash]

This problem has a much easier proof. If you draw triangle ACE, it will be surrounded by three other triangles inside the hexagon; together, they cover the entire hexagon. Likewise, triangle BDF is surrounded by three other triangles. The sum of areas of these surrounding triangles are equal in the two cases, hence the areas of ACE and BDF are equal.

[vincfr]

Nice proof, but the proof of the lemma is incomplete, because there are 2 rather different cases for P outside of the triangle (visible when you extend the edges of the triangles to straight lines: there are 2 kinds of regions outside of the triangle). Moreover, you could define the oriented area of a triangle with a cross product (as other readers suggested), and I think that you would not need to distinguish cases.

[txikitofandango]

The area of a triangle is half the cross product of two of its sides. So, using these coordinates, just show that AC x AE = BD x BF.

The six lines that make the hexagon are (a:b:c), (d:e:f), (g:h:i), (a:b:j), (d:e:k), (g:h:l), where (a:b:c) means Ax+By+C=0, etc. Note that opposite sides share the first two coordinates, because they're parallel. Now, point A is (bl-ch, cg-al)/(ah-bg), point B is (bf-ec, cd-af)/(ae-bd), and so on. The vector AC turns out to be ( (ei-fh)/(dh-eg) - (bl-ch)/(ah-bg), (fg-di)/(dh-eg) - (cg - al)/(ah-bg) . ... and so on and so on.

This takes a while, but it works. This method works for non-convex hexagons as well.

[Reliquancy]

Cool that if you have a convex polygon and a point p, the areas of the triangles made by each side of the polygon and p only equal the area of the polygon if p is inside the polygon. So you have an equation for the region inside the polygon. You can use the shoelace theorem to write out the equation in terms of the vertices of the polygon, you have to square or abs terms to keep the areas positive though..

[tomatrix]

What is it with Hungary and math contests? Are they like the origin of them?

[johnrstern]

Note because of parallel sides
|AC| = |DF|, |EA| = |BD|, and |CE| = ||FB|. Consequently triangles "ACE"and ""DFB" are congruent and hence have the same areas. No need for any heavy machinery.

[zarachameau]

Interesting. Theory on hexagonal network is very rare.

You used the parallelograms, but each diameter is 2 times the respective parallel edge. So there are 3 equal triangles from either side. Areas may be calculated this way also. For me, I found very difficult to use the parallellograms. Your demonstration give me a good idea how to do it, however.

The particularity of the hexagonal network is thet it is connected by the vertices, rather than by the edges, as the equilateral one, all the angles at 60°, makes us think. It is because it is the only one that is connected also by the edges.

I have studied the hexagonal network, and one day, I made a diagram of it with a resource that I found on the Internet, using the grid sheet and only 3 colors, which were only possible with what I had. But it gives a good idea of what it is, with any 3 triangles and a possibility of covering the field with 6 colors, plus the white one for the blanks (the holes), that makes 7 colors, in all.

But I think 3 more colors can rather be used for the iteration of each triangle, as holes, what would do 9 colors in all, then. And maybe doubled, also, as opposite holes, as the same triangle is itself opposite symetrically in the hetwork, for a total of 12 colors, now, but it may be experimented, I suppose, to see if it fits well. I just imagine it, visually.

That surpasses largely the classic theory of 4 colors, generally used to make geographic maps.

My diagram of the hexagonal network is in an article on my blog, La vie d'art triste, titled " Hexagone-réseau : exemple de construction et de visualisation". here :

[prathmeshraut]

Hey Micheal there are some comments 1months and weeks ago how are they getting ur video early?

[TedHopp]

I haven't watched the entire video yet, but the proof of the lemma in the second case is needlessly complicated. It's enough to note that the area of triangle ABC is the area of the quadrilateral PCAB minus the area of the triangle PCB, and the area of the quadrilateral PCAB is the sum of the areas of triangles PCA and PAB. Converting to signed areas then proves the case; no need to introduce the point O and all those subtriangles.

[manucitomx]

I love geometry. And yes, this is a good place to stop.

[srajanverma]

but isnt triangle ABC same as triangle ACB.... can anyone explain...?

[CM_France]

Hi,

For fun:

1 "let's go ahead and",

1 "so let's may be go ahead and".

[maxwellsequation]

Hello time travellers in comment section!
Nice to see u

[random-tdtf]

Prove the “fact“ wrong :
“Good Place To Stop” gets the max likes on this channel