Visual Group Theory, Lecture 5.2: The orbit-stabilizer theorem

Visual Group Theory, Lecture 5.2: The orbit-stabilizer theorem

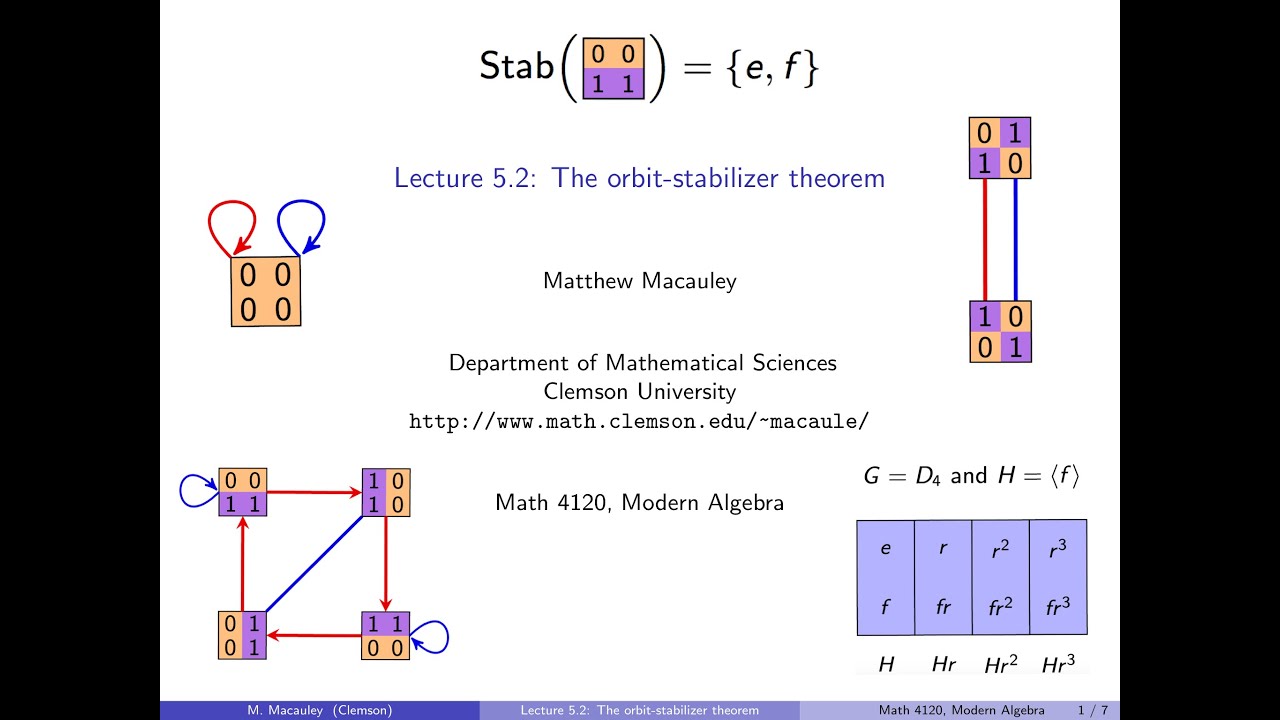
Suppose a group G acts on a set S. The orbit of s in S is the collection of states (in S) reachable from s. The stablizer of s is the set of elements (in G) that fix s. The orbit-stabilizer theorem says that |G|=|Orb(s)|*|Stab(s)|, where |Orb(s)| is the size of the orbit containing s, and |Stab(s)| is the size of the stabilizer of s. This is one of the central results on groups actions. To prove this, we first establish that Stab(s) is always a subgroup of G, and then exhibit a bijections between Orb(s) and the cosets of Stab(s). In other words, we prove that two elements in G send s to the same place iff they're in the same coset.

[carolynrigheimer]

Many, many thanks, Professor. Your lectures have explained things I could not understand and I am in grad school. I wish I had you for my first abstract algebra class.

[joetursi]

Dear Professor Macauley, Thanks you, thank you, thank you for your very lucid lecture 5.2.  The orbit of an element and the element stabilizer has long been unclear to me, at least when I look at their formal definitions. Again, when appears difficult in definition, is really something easy to understand when described pictorially and with simple language. Students often have the same problem with function and their notation.I have paused your lecture to tell you how delighted I am to have discovered your lectures and will continue to seek them out!Many thanks, Joe Tursi

[teine]

Very good lectures. I had earlier problem to understand the concept of actions, orbits and stabiliziers, but these videos helped a lot.

[samuelschlesinger]

In the slide labeled: Orbits, Stablizers, and Fixed Points, you write phi : G -> S when you mean phi : G -> Perm(S).

[shacharh]

a G action on S is not a function from G to S, it's a function from GxS to S

[silverskonisburg]

thank you so much
my university keep telling me note without picture only concept

[algebraicgirl]

Timemarks for anyone who needs them.

00:00 Overview
00:15 Orbits, stabalizers and fixed points
09:20 Orbits ans stabilizers
14:54 The Orbit-Stabilizer Theorem
27:04 Next lecture...

[joetursi]

Hi Professor, Just a big thank you for a very easy to understand proof., in comparison to the same proof in texts. Notation can be very confusing for the novice. Just looking a the notation for a left coset can be daunting, as least, for me.

[musicarroll]

Phi cannot be a homomorphism from G to S. S is not a group, only a set.

[elsomath]

please help me Prof.. How to compute stabilizer and orbit of matrices with manual method, that is without software. I'm waiting for your answer.