filmov
tv
Intro Complex Analysis, Lec 16, Taylor Polynomials, Complex Exponential, Trig & Hyperbolic Functions
Показать описание
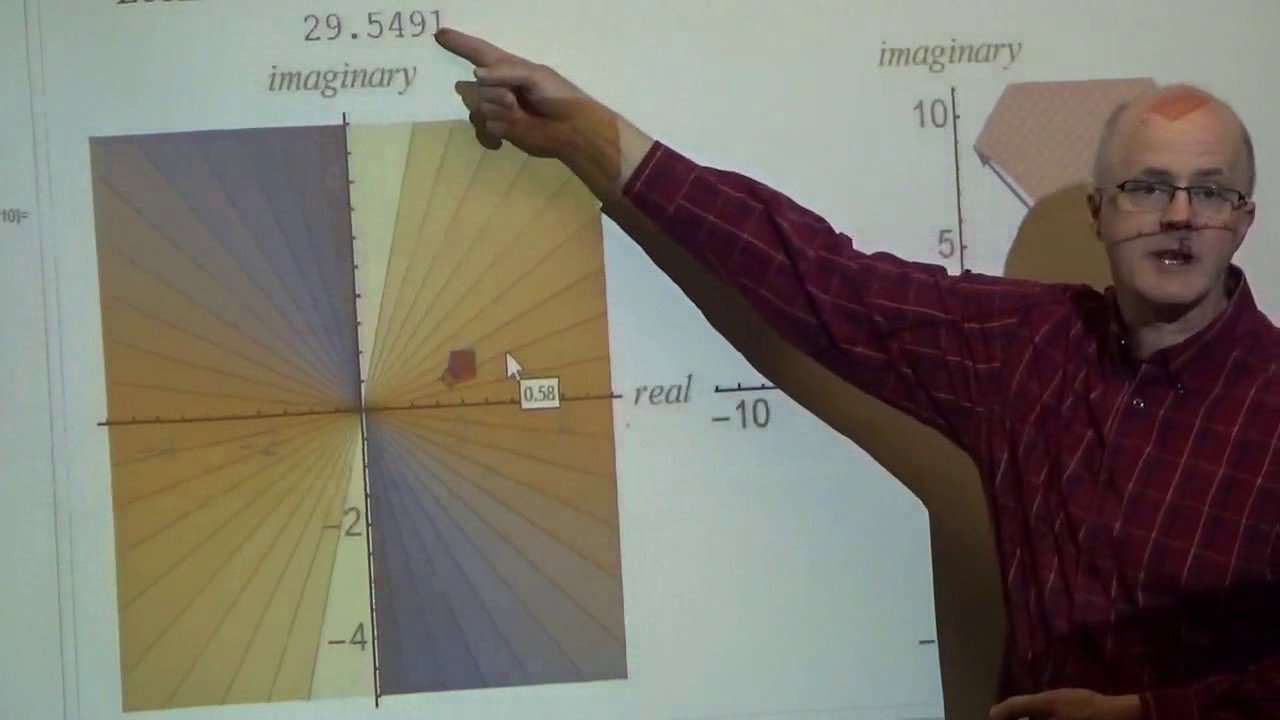
Lecture 16. (0:00) Goals and a demonstration of what happens near where the derivative of an analytic function is zero. (5:42) Visualizing the amplitwist based on the modulus of the derivative and the argument of the derivative (based on Tristan Needham's "Visual Complex Analysis"). (9:35) Find a (finite) Taylor expansion of a polynomial function about z = 2 in two ways: 1) substitution, 2) Taylor's formula. (20:07) Comments about functions versus multi-valued functions. (21:20) The complex exponential function: formula, periodicity, mapping properties. (28:05) The complex cosine and sine functions: derivatives, identities, modulus of cosine along the imaginary axis. (39:34) The complex hyperbolic functions: identities, relationships to trigonometric functions, geometric/numerical demonstration of sin(iz) = i*sinh(z). (46:15) Introduction to the complex logarithm
AMAZON ASSOCIATE
As an Amazon Associate I earn from qualifying purchases.
 0:51:44
0:51:44
 0:57:58
0:57:58
 0:54:09
0:54:09
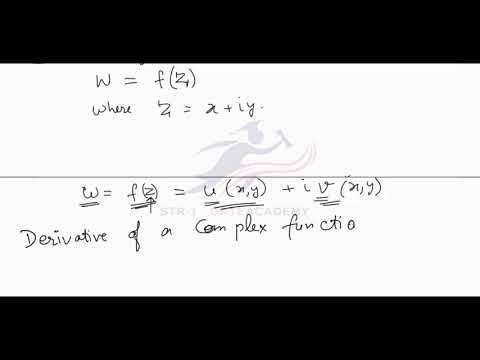 0:45:51
0:45:51
 0:50:51
0:50:51
 1:00:48
1:00:48
 0:56:18
0:56:18
 0:03:24
0:03:24
 0:54:39
0:54:39
 0:09:47
0:09:47
 0:59:16
0:59:16
 0:57:31
0:57:31
 0:58:57
0:58:57
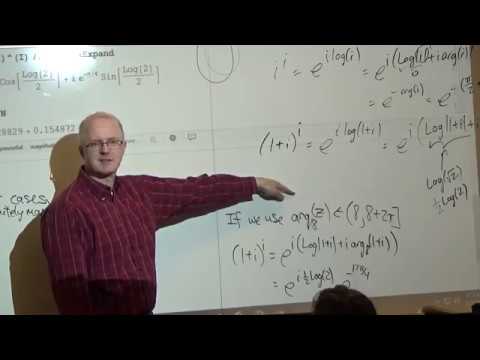 0:55:34
0:55:34
 0:48:44
0:48:44
 1:21:54
1:21:54
 0:57:44
0:57:44
 0:55:47
0:55:47
 0:55:04
0:55:04
 0:54:17
0:54:17
 0:41:49
0:41:49
 0:36:30
0:36:30
 0:12:34
0:12:34
 0:50:47
0:50:47