filmov
tv
Intro Complex Analysis, Lec 24, Integration, Cauchy-Goursat Theorem, Cauchy Integral Formula

Показать описание
Lecture 24. (0:00) Project idea (flows for vector fields, which model fluid flows, though not necessarily accurately). (5:49) Review the basics of complex integration of a complex valued functions over an oriented contour. The integral can be defined in terms of a Riemann sum. It is calculated using a parameterization. Ultimately integrate f(z(t))*z'(t). It is good to relate this to two real line integrals (contour integrals). (16:25) Review the Cauchy-Goursat Theorem (can also just called Cauchy's Theorem or Cauchy's Integral Theorem) for the complex integral of an analytic function over a simple closed contour in a simply connected domain. (19:50) Idea of the proof of a weaker version of the theorem using Green's Theorem and assuming that the derivative f'(z) is continuous (relate to double integrals of the scalar curl of each vector field). Also apply the Cauchy-Riemann equations to finish the idea of the proof. (26:31) The vector fields are actually conservative (independent of path), so they have potential functions. The real and imaginary parts of an antiderivative F(z) of f(z) will be potential functions. (31:53) Let f(z) be an analytic function. Explore what happens when you integrate f(z)/(z - z0) over a simple closed contour containing z0. Need to use the Deformation Invariance Theorem (which is equivalent to the Cauchy-Goursat Theorem). Ultimately derive the Cauchy Integral Formula. This allows you to represent the value of an analytic function at a point in terms of its values along some simple closed contour containing the point. It is very useful for: 1) evaluating integrals, 2) studying and proving facts about analytic functions. You can also prove the Fundamental Theorem of Algebra with it. It can also be used to prove that analytic functions are infinitely differentiable. (45:56) Rewrite the Cauchy Integral Formula and differentiate the integral by differentiating the integrand. We can also continue differentiating to ultimately derive the generalized Cauchy Integral Formula.
AMAZON ASSOCIATE
As an Amazon Associate I earn from qualifying purchases.
 0:54:17
0:54:17
 0:57:58
0:57:58
 0:56:18
0:56:18
 0:57:31
0:57:31
 0:54:39
0:54:39
 0:48:40
0:48:40
 0:54:39
0:54:39
 0:59:16
0:59:16
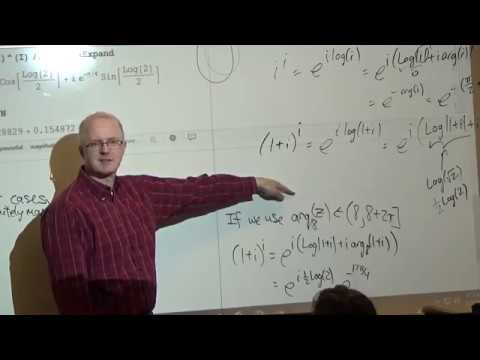 0:55:34
0:55:34
 0:54:09
0:54:09
 0:55:47
0:55:47
 0:54:33
0:54:33
 0:09:53
0:09:53
 0:53:35
0:53:35
 0:58:57
0:58:57
 1:00:48
1:00:48
 0:54:06
0:54:06
 0:57:44
0:57:44
 0:55:42
0:55:42
 0:53:29
0:53:29
 0:55:15
0:55:15
 0:25:42
0:25:42
 0:52:25
0:52:25
 0:04:48
0:04:48