filmov
tv
Intro Complex Analysis, Lec 12, Cauchy-Riemann Eqs (Rectangular & Polar), Intro Harmonic Functions
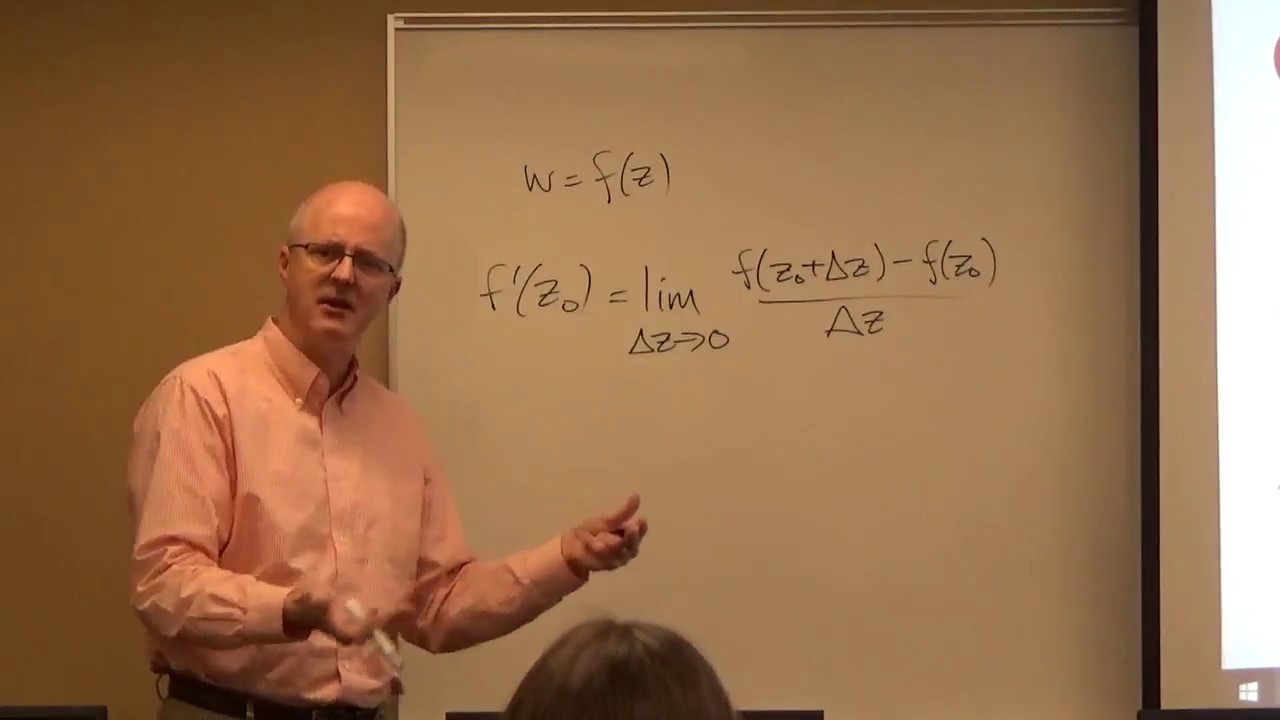
Показать описание
Lecture 12.
(0:00) Announcements.
(0:22) Lecture topics.
(0:59) Review differentiability and analyticity.
(3:19) Derive the Cauchy-Riemann equations symbolically (their necessity when differentiability is assumed). Mention the sufficiency of the Cauchy-Riemann equations when the partial derivatives are continuous.
(16:28) Check the Cauchy-Riemann equations on Mathematica for complicated examples.
(24:53) Geometric meaning of the Cauchy-Riemann equations with contour maps (of level curves) on Mathematica, both in terms of local linearity and partial derivatives as rate of change, and in terms of orthogonal trajectories.
(33:26) The polar form of the Cauchy-Riemann equations. Derive with the Chain Rule from Multivariable Calculus and the conversion equations for polar coordinates.
(47:11) Attempt to confirm this using level curves and linear approximations.
(55:25) Analytic functions have real and imaginary parts that satisfy Laplace's equation. They are called harmonic functions.
AMAZON ASSOCIATE
As an Amazon Associate I earn from qualifying purchases.
Intro Complex Analysis, Lec 12, Cauchy-Riemann Eqs (Rectangular & Polar), Intro Harmonic Functio...
Intro Complex Analysis, Lec 11, Areas of Images, Differentiability, Analyticity, Cauchy-Riemann Eqs
Intro Complex Analysis, Lec 13, Preimages, Laplace's Equation, Harmonic and Analytic Functions
Complex Analysis 1 | Introduction
Intro Complex Analysis, Lec 9, Facts to Recall, Animations, Continuity Proofs (z^2 and 1/z)
Introductory Complex Analysis, Lec 36, Review for Complex Analysis Final Exam
Intro Complex Analysis, Lec 15, Review Analytic Functions, Amplitwist Concept, Harmonic Functions
Intro Complex Analysis, Lec 16, Taylor Polynomials, Complex Exponential, Trig & Hyperbolic Funct...
Intro Complex Analysis, Lec 25, Cauchy Integral Formula, Applications, Liouville's Theorem
Intro Complex Analysis, Lec 14, Preimages, Mathematica, Maximum Principle (Harmonic), Polynomials
Intro Complex Analysis, Lec 23, Real Line Integrals and Applications, Complex Integration
Intro Complex Analysis, Lec 19, Complex Powers, Inverse Trigonometric Functions, Branch Cuts
Intro Complex Analysis, Lec 20, Invariance of Laplace's Eq, Real & Im Parts of Complex Inte...
Complex Analysis 02: Mappings
Intro Complex Analysis, Lec 32, More Laurent Series, Review Integrals & Cauchy Integral Formula
Intro Complex Analysis, Lec 31, Laurent Series, Poles of Complex Functions, Essential Singularities
Intro Complex Analysis, Lec 35, Residue Theorem Examples, Principal Values of Improper Integrals
Mod-07 Lec-20 Introduction to Hurwitz\'s Theorem for Normal Convergence of Holomorphic Function...
Intro Complex Analysis, Lec 26, Sequences and Series of Functions, Maximum Modulus on Mathematica
Intro Complex Analysis Lec 30, Laurent Series Calculations, Visualize Convergence on Mathematica
Intro Complex Analysis, Lec 7, Exponential & Reciprocal Maps, Domains, Derivative Limit Calculat...
Derivatives of Complex Valued Functions - Lec 12
Intro Complex Analysis, Lec 17, Complex Logarithm, Functions as Sets, Multivalued Functions
Mod-11 Lec-32 Introduction to Marty's Theorem
Комментарии
 0:57:58
0:57:58
 0:59:16
0:59:16
 0:57:43
0:57:43
 0:09:47
0:09:47
 0:57:31
0:57:31
 0:56:18
0:56:18
 1:00:48
1:00:48
 0:51:44
0:51:44
 0:48:40
0:48:40
 0:56:12
0:56:12
 0:54:39
0:54:39
 0:55:34
0:55:34
 0:54:09
0:54:09
 0:12:34
0:12:34
 0:55:15
0:55:15
 0:55:30
0:55:30
 0:53:29
0:53:29
 0:43:55
0:43:55
 0:53:35
0:53:35
 0:52:25
0:52:25
 0:55:15
0:55:15
 0:22:37
0:22:37
 0:54:06
0:54:06
 0:44:07
0:44:07