filmov
tv
Intro Complex Analysis, Lec 33, Integrating 1/(1+z^2), Mathematica programming, Residue Thm intro

Показать описание
Introduction to Complex Analysis Course, Lecture 33. Sorry that the camera has trouble focusing the first 2 minutes. (0:00) Plan for the last 2 weeks. (2:11) Consider whether God's plan for your life could include exploring complex analysis further. (3:26) Antiderivative of 1/(1+x^2) and graphs. (6:10) Area under the graph of 1/(1+x^2) evaluated as an improper integral which is defined as the sum of two improper integrals (and these integrals do converge). (10:39) Integrate 1/(1+z^2) over various closed contours (circles) using Mathematica to visualize the corresponding vector fields (based on expanding the function in terms of its real and imaginary parts). Emphasize important points about Mathematica programming (and use of Manipulate, Grid, Show, StreamPlot, VectorPlot, and ParametricPlot). (39:46) The integral around a pole of the function will be nonzero. Use the Method of Partial Fractions and the geometric series formula to find the Laurent expansion of f(z) = 1/(1 + z^2) about z = i to get an answer of pi. (49:24) Relate the answer of pi to the residue of f(z) = 1/(1 + z^2) at z = i using the Residue Theorem. (52:19) Why is the improper integral of f(z) = 1/(1 + z^2) from minus infinity to plus infinity equal to pi? Also include a brief discussion of the Cauchy principal value of an improper integral.
AMAZON ASSOCIATE
As an Amazon Associate I earn from qualifying purchases.
Комментарии
 0:54:39
0:54:39
 0:57:58
0:57:58
 0:03:32
0:03:32
 0:56:18
0:56:18
 0:55:47
0:55:47
 0:04:56
0:04:56
 0:44:56
0:44:56
 0:55:15
0:55:15
 0:53:29
0:53:29
 0:57:43
0:57:43
 0:01:33
0:01:33
 0:00:16
0:00:16
 0:54:09
0:54:09
 0:18:47
0:18:47
 0:58:57
0:58:57
 0:04:59
0:04:59
 0:57:31
0:57:31
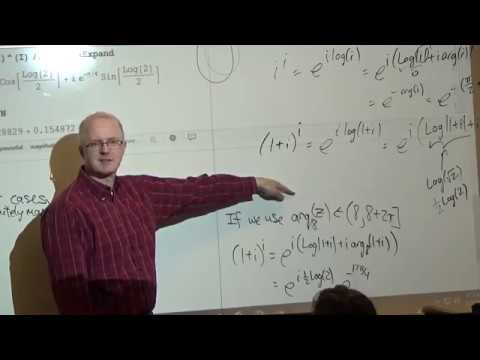 0:55:34
0:55:34
 0:16:52
0:16:52
 0:03:01
0:03:01
 0:48:40
0:48:40
 0:51:35
0:51:35
 0:58:17
0:58:17
 0:52:25
0:52:25