filmov
tv
Introductory Complex Analysis, Lec 36, Review for Complex Analysis Final Exam

Показать описание
Introduction to Complex Analysis Course, Lecture 36.
(0:00) We will review for the final exam today. Time for the final exam.
(1:45) We will go through old exams.
(3:04) Complex arithmetic problem, including use of Euler's identity.
(4:40) Use properties of the modulus of a complex number to simplify the modulus of a quotient of products.
(6:06) Identify a set (a punctured disk of radius 4) as open, closed, both, or neither; connected or not; domain or not; bounded or not.
(10:02) Describe the image of a line under the complex mapping w = f(z) = z^2.
(15:19) Plot some a point and related points ("z bar", -z, and 1/z) in the complex plane and graph a set of points in the complex plane.
(19:16) Find all the complex cube roots of a negative real number (-64, in this case). It's helpful to write it in polar form. Be able to write the roots in either rectangular form or polar form.
(24:54) Find the real and imaginary parts of a complex analytic mapping and find the corresponding real planar mapping. Also verify that the Cauchy Riemann equations hold.
(26:44) Compute an antiderivative of (cos(theta))^5 using the complex form of the cosine function and the binomial theorem, plus some simplification.
(30:29) Find the area of the image of the unit disk under a complex mapping by doing a change of variables with a double integral (use the Jacobian determinant of the corresponding real mapping). It's best to do the double integral using polar coordinates.
(33:48) Prove that a certain set is an open set.
(34:37) Do an epsilon delta proof of a certain limit fact involving a quadratic.
(35:04) Evaluate special values of various function: a) Principal value of the logarithm (or another branch of the multivalued logarithm function). b) Principle value of (1 + i)^(i) (the i power). Relate it to the exponential function and logarithm. c) Find Sin(1 + i). d) Find Cos(2i).
(39:27) Use Tristan Needham's amplitwist concept (the derivative as an amplitwist) to approximate how a complex analytic mapping dilates and rotates small vectors near a given point.
(41:36) Be able to verify Laplace's equation for a harmonic function (which is the real part of an analytic function).
(41:46) Use Partial Fractions to break apart a rational function and find the residue of that function at a pole. Also be able to calculate it using the limit equation (also involving a derivative).
(44:29) Compute a complex integral in two ways: 1) with a parameterization, and 2) with an antiderivative and the Fundamental Theorem of Calculus.
(46:15) Write a complex analytic mapping in polar coordinates with Euler's identity and verify the Cauchy-Riemann equations in polar coordinates.
(46:42) Find a harmonic function satisfying certain constant boundary conditions on an annulus centered at the origin.
(46:50) Use Clairaut's theorem to verify that a partial derivative of a harmonic function is also a harmonic function.
(47:03) Various true/false questions.
(47:13) Compute a complex integral in two ways: 1) with a parameterization, and 2) with an antiderivative and the Fundamental Theorem of Calculus.
(48:03) Use the Ratio Test to confirm a certain real series converges.
(48:12) Find the global maximum of a harmonic function on a closed disk by parameterizing the boundary (the Extreme Value Theorem and the Maximum Principle are Relevant).
(48:33) More true/false questions.
(48:36) Use the Cauchy integral formula and generalized Cauchy integral formula to compute complex line integrals.
(49:55) If the imaginary part of an entire function is bounded above, then the function must be constant (apply Liouville's theorem to a modified form of the function).
(50:34) Use Taylor series to find Laurent series. Find a Taylor series and a Laurent series. Find the order of a pole.
(51:28) Be able to calculate residues and apply the Residue theorem: in particular, to calculate improper integrals.
(51:50) Visualize complex integration in terms of line integrals of vector fields and also in terms of the real and imaginary parts of an antiderivative (and the antiderivatives are analytic on domains obtained by branch cuts)
AMAZON ASSOCIATE
As an Amazon Associate I earn from qualifying purchases.
Комментарии
 0:56:18
0:56:18
 0:06:03
0:06:03
 0:06:49
0:06:49
 0:40:23
0:40:23
 0:49:21
0:49:21
 0:57:31
0:57:31
 0:35:00
0:35:00
 0:46:14
0:46:14
 0:48:40
0:48:40
 0:03:32
0:03:32
 0:58:57
0:58:57
 0:59:21
0:59:21
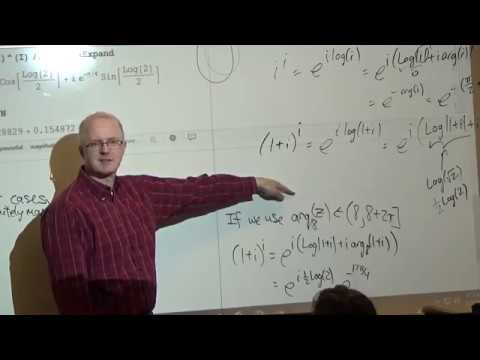 0:55:34
0:55:34
 1:00:48
1:00:48
 0:25:56
0:25:56
 0:56:12
0:56:12
 0:36:54
0:36:54
 0:49:13
0:49:13
 0:50:47
0:50:47
 0:51:13
0:51:13
 0:49:37
0:49:37
 0:47:37
0:47:37
 2:30:54
2:30:54
 0:59:16
0:59:16