filmov
tv
Proving Uniform Continuity using ε-δ

Показать описание
Help me create more free content! =)
Today we are going to proof uniform continuity of the funktion cos(x)+x. For this we make use of the abstract epsilon delta definition and use some spicy integral approximations to deal with everything. Enjoy! =D
--------------------------------------------------------------------------------
Wanna send me some stuff? lel:
Postfach 60 06 03
14406 Potsdam
Brandenburg
Germany
--------------------------------------------------------------------------------
Today we are going to proof uniform continuity of the funktion cos(x)+x. For this we make use of the abstract epsilon delta definition and use some spicy integral approximations to deal with everything. Enjoy! =D
--------------------------------------------------------------------------------
Wanna send me some stuff? lel:
Postfach 60 06 03
14406 Potsdam
Brandenburg
Germany
--------------------------------------------------------------------------------
Proving Uniform Continuity using ε-δ
Proof: f(x) = |x| is Continuous using Epsilon Delta Definition | Real Analysis Exercises
PROVE UNIFORMLY CONTINUOUS FUNCTION
The Sum of Uniformly Continuous Functions is Uniformly Continuous Proof
Continuity of a Function | ε-δ | Prove that for f(x)=x^2, f is uniformly continuous on [0,3].
Lipschitz Functions and Uniform Continuity
Continuous and Uniformly Continuous Functions
What is Uniform Continuity?
Proof: f(x) = x is Continuous using Epsilon Delta Definition | Real Analysis Exercises
Epsilon Delta Continuity (Example 4): x^3
Using the Epsilon-Delta Definition to Prove Continuity
proving x^2 is continuous using the epsilon delta definition
Proof: sqrt(x) is Continuous using Epsilon Delta Definition | Real Analysis Exercises
Proof that f(x) = 1/x is Continuous on (0, infinity) using Delta-Epsilon
Proof: e^x is Continuous using Epsilon Delta Definition | Real Analysis Exercises
Prove x² is continuous under 60 seconds!
402.4Y3 What Is Uniform Continuity?
Uniform Continuity Part 1
Proof that Sqrtx is uniformly continuous
Proving continuity -- finding delta
Proof that f(x) = 1/x is not Uniformly Continuous on (0,1)
uniform continuity - example - proof
Prove that the function f(x) = 1/x^2 is uniformly continous on [a, infinity)
402.4Y8 Proving a Function Is (Not) Uniformly Continuous
Комментарии
 0:11:31
0:11:31
 0:04:19
0:04:19
 0:09:47
0:09:47
 0:08:02
0:08:02
 0:04:32
0:04:32
 0:05:26
0:05:26
 0:05:13
0:05:13
 0:06:23
0:06:23
 0:04:46
0:04:46
 0:06:59
0:06:59
 0:04:54
0:04:54
 0:09:35
0:09:35
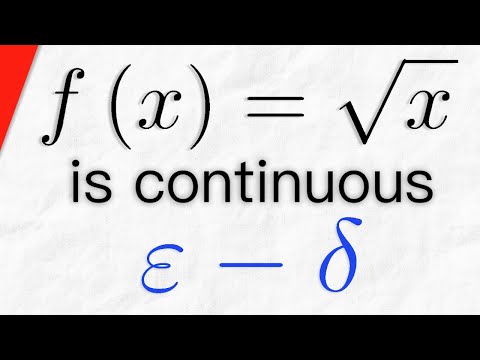 0:09:22
0:09:22
 0:09:56
0:09:56
 0:14:36
0:14:36
 0:00:48
0:00:48
 0:11:49
0:11:49
 0:16:00
0:16:00
 0:16:55
0:16:55
 0:19:49
0:19:49
 0:04:40
0:04:40
 0:17:03
0:17:03
 0:13:57
0:13:57
 0:17:07
0:17:07