Proving continuity -- finding delta

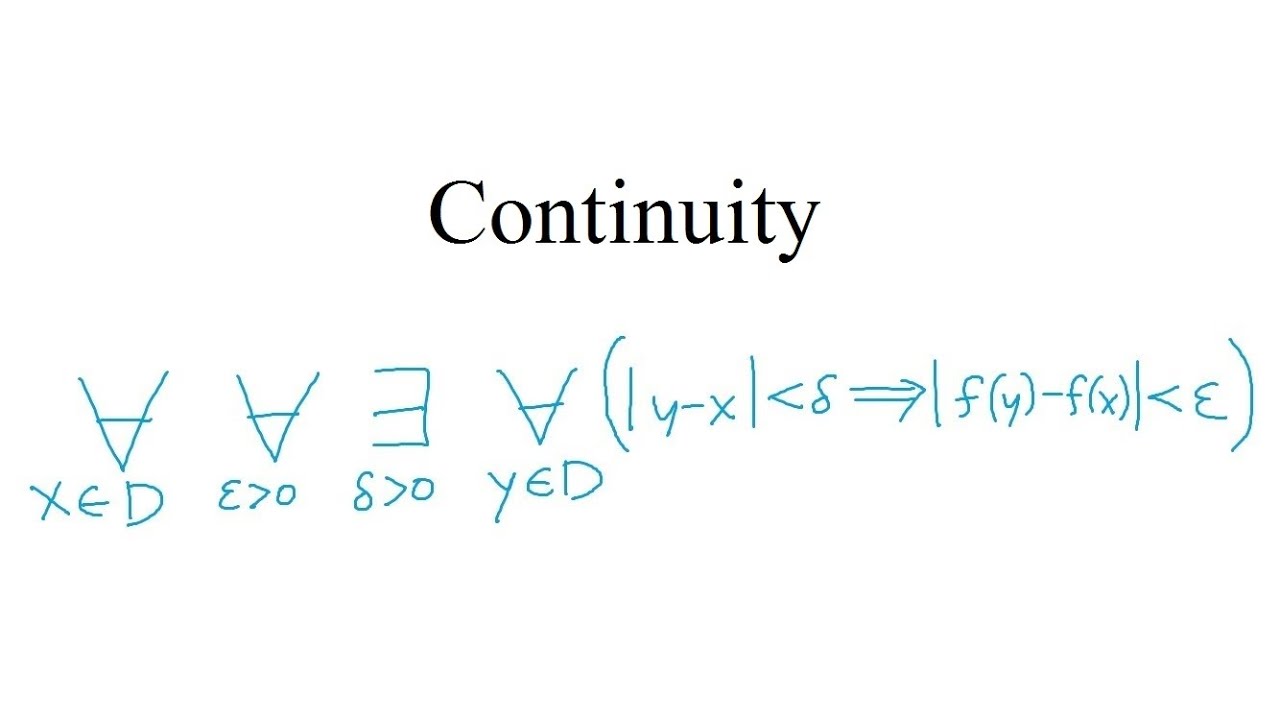
Показать описание

In this video we use the epsilon delta criterion to prove the continuity of two example functions. The emphasis is on understanding how to come up with the required delta value.

Рекомендации по теме

Комментарии

There is a small mistake in the video at 9:04. I gave as the reason for using the "less than or equals" sign (as opposed to the stricter "less than" sign) that |x - y| might be zero. What I should have said is that |x + y| might be zero. The proof is still correct; just the stated justification was incorrect.

mathaha

seriously I was so frustrated because I didn't understand the procedure to show continuity, after your video a lot got so much clearer thank you so much!

majamuster

Excelent video. Thank you so much. I needed to remember how to do these proofs and you explained them flawlessly. Never really understood why we could select a "first delta", but now I know.

julioenciso

I REALLY appreciate this video! You have made this topic crystal clear to me, so thank you very much.

edwardhartz

Awesome video man, was lost before this, keep them coming!
It also helps that you talk like Bob Ross

creestee

Hello, i understand the whole video, but something bothers me. How are we allowed to pick a value for delta ? I mean, i thought this is what we were trying to find ? Thanks.

Gaelrenaultdu

Thanks for this, its been very helpful in clarifying the process to solving these problems.

WillPrice

Hello, isn't delta supposed to be less than min{1, epsilon/1 + |2x|} and not equal to it ?

Gaelrenaultdu

Excellent video, thanks so much! At 10:20 you have that delta( |y - x| + |2x| ) = delta(delta + |2x|). Could you tell me how you got that to be so? thanks again!

jvickers

Amazing! Thank you so much. Good to finally understand this

thedan

I don't really get why we chose delta to be the minimum of (1, Epsilon/(1+2|x|)). I know that we need our delta to be less or equal to 1, but if 1 < (Epsilon / (1+2|x|)) Delta will then be equal to one, and our proof won't be valid anymore..?

flyur

Oh my god thank you, my textbook provides little to no detail as to how you do this.

StellaBellabreeze

This is uniform continuity as opposed to just continuity correct?

cgxyz

In the first proof you made delta depend on x and y. x is the point you are investigating, shouldn't delta depend at most on x instead of also on y?

ElizaberthUndEugen

This video was super helpful. Thanks!!

aprilcrandall

hi, on your first proof why epsilon becomes equal to |f(y)-f(x)| instead of epsilon being less than |f(y)-f(x)|? it's the last part written in green on 5:34

joaquinbrandan

superb!!! I got it. you made it easy for me.thanks a lot!!

vikrantraghav

Finally, a math teacher where you can hear his saliva

hioman

Thanks! Great video, very helpful! :)

grup

how we can say 3delta is equal to ephsilon

sajadbarbra

Proving continuity -- finding delta

Proving continuity -- finding delta

Finding the Delta that Works for the Proof of Continuity

Using the Epsilon-Delta Definition to Prove Continuity

Finding delta from a graph and the epsilon-delta definition of the limit (KristaKingMath)

Proof of a Limit Value Using Epsilon and Delta

Finding a Delta Given an Epsilon

how to easily write the epsilon-delta proofs for limits

Proving Continuity at a Point Using an Epsilon-Delta Argument

Uniform Continuity Explained | Real Analysis

Finding Delta That Works for Continuity Proof (example 2)

proving x^2 is continuous using the epsilon delta definition

Epsilon Delta Limits in 4 Minutes

Proof that f(x) = 1/x is Continuous on (0, infinity) using Delta-Epsilon

Epsilon Delta Continuity (Example 4): x^3

This is the Epsilon Delta Definition of Continuity | Real Analysis

Limits and Continuity: Epsilon Delta Proofs

Epsilon Delta Continuity (Example 6): 1/x

3 Step Continuity Test, Discontinuity, Piecewise Functions & Limits | Calculus

Prove continuity using epsilon-delta definition.

epsilon-delta definition ultimate introduction

Epsilon Delta Continuity (Example 7): Square Root

Calculus - Find the limit of a function using epsilon and delta

[1] Epsilon-Delta definition of the continuity of a function at a point

Limits, L'Hôpital's rule, and epsilon delta definitions | Chapter 7, Essence of calculus