Linear Algebra Example Problems - Matrix Row Space Basis and Dimension

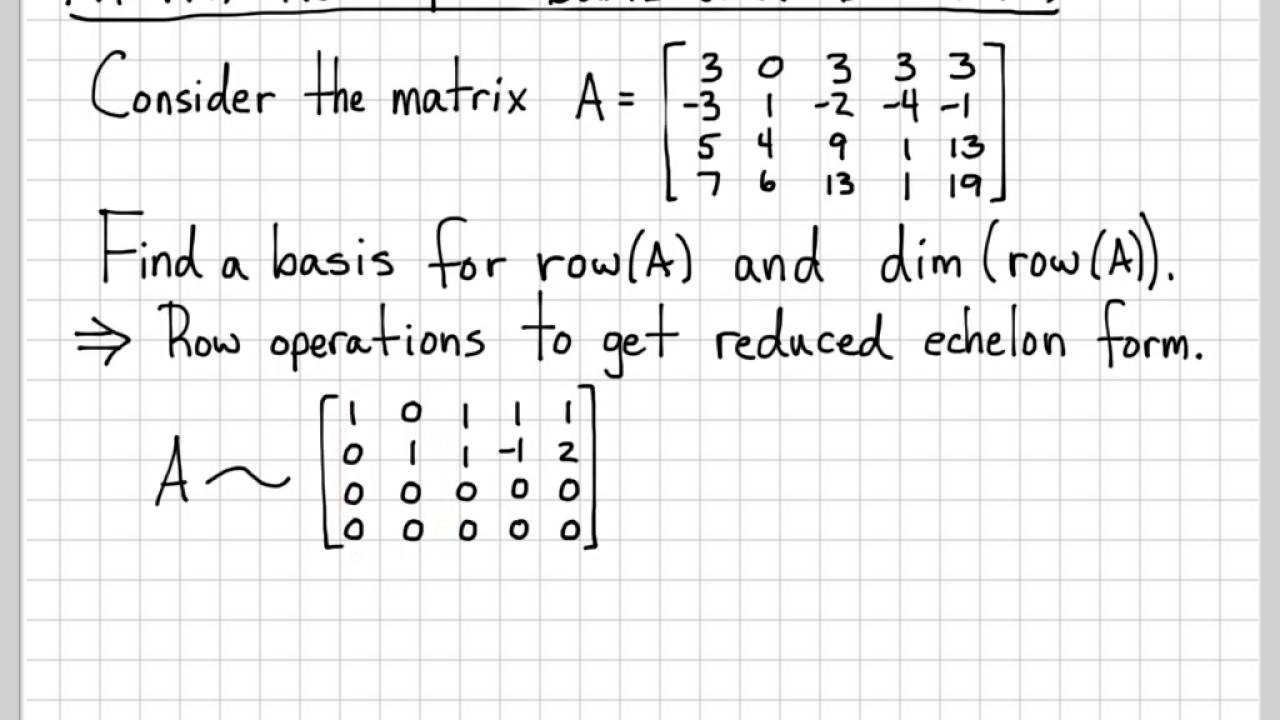
preview_player
Показать описание


The row space of a matrix consists of all linear combinations of the matrices rows. In this video we show how to to find a basis to describe this subspace.

Simply perform row operations on A to obtain a reduced echelon form of the matrix. Identify any rows that AREN'T all zeros. These non-zero rows then form the basis vectors for the row space of the original matrix.

  1. Adam Panagos
  2. matrix row space dimension
  3. how to find row space basis
  4. matrix row space basis
  5. row space basis
  6. row space basis and column space basis
Рекомендации по теме
Linear Algebra Example 0:04:48

Linear Algebra Example Problems - Subspace Example #1

Linear Algebra Example 0:04:47

Linear Algebra Example Problems - Vector Space Basis Example #1

Linear Algebra Example: 0:12:47

Linear Algebra Example: Span Questions

Linear Algebra Example 0:04:31

Linear Algebra Example Problems - Spanning Vectors #1

Linear Algebra Example 0:03:53

Linear Algebra Example Problems - Linear Combination of Vectors #2

Linear Algebra Example 0:05:52

Linear Algebra Example Problems - Finding 'A' of a Linear Transformation #1

Linear Algebra 7 0:10:56

Linear Algebra 7 | Examples for Subspaces

linear algebra vector 0:30:16

linear algebra vector space (25 examples)

hermitian and skew 0:03:38

hermitian and skew hermitian matrix | hermitian and non hermitian matrix

Linear Algebra Example 0:07:40

Linear Algebra Example Problems - Finding 'A' of a Linear Transformation #2

Linear Algebra Example 0:04:42

Linear Algebra Example Problems - Linear Transformation Ax #1

Linear Algebra Example 0:05:54

Linear Algebra Example Problems - Coordinate System Representation Example #1

Linear Algebra Example 0:04:20

Linear Algebra Example Problems - One-to-One Linear Transformations

Linear Algebra Example 0:05:02

Linear Algebra Example Problems - Vector Space Basis Example #2

Linear Algebra Example 0:08:41

Linear Algebra Example Problems - Change of Coordinates Matrix #1

Linear Algebra Example 0:03:37

Linear Algebra Example Problems - Linear Combination of Vectors #1

Linear Algebra Example 0:04:58

Linear Algebra Example Problems - Linearly Independent Vectors #1

Linear Algebra Example 0:04:13

Linear Algebra Example Problems - Eigenvalue Computation #1

Linear Algebra Example 0:04:41

Linear Algebra Example Problems - Diagonalizing a Matrix

Linear Algebra Example 0:05:20

Linear Algebra Example Problems - Onto Linear Transformations

Linear Algebra Example 0:05:46

Linear Algebra Example Problems - Subspace Example #3

Linear Algebra Example 0:06:14

Linear Algebra Example Problems - A Polynomial Subspace

Linear Algebra Example 0:09:10

Linear Algebra Example Problems - Subspace Example #4

Linear Algebra Example 0:05:27

Linear Algebra Example Problems - Coordinate System Representation Example #2

Комментарии
Автор

this was exactly what i needed to get through my homework, thanks so much

disaster
Автор

why do you take rows out of the rref of A for the row space but the columns of A for the column space?

stijndhondt
Автор

Why in your Column basis video, you take the basis of the original matrix A but in this one you take the row basis from the equvi. of A?

brittanielaird
Автор

thanks bud, very clear. all the best.

romaion
Автор

How do we know that the non zero rows are linearly independent?

Zuwwar