filmov
tv
Linear Algebra Example Problems - Linear Combination of Vectors #1

Показать описание
Given the vectors v1, v2, and v3, we see if the vector b can be written as a linear combination of the vectors.
This can be easily determined by constructing an augmented matrix, performing row operations, and finding the coefficients such that a1*v1 + a2*v2 + a3*v3 = b.
If values for a1, a2, and a3 can be found, then b is a linear combination of {v1,v2,v3} and we say that b is in the Span{v1,v2,v3}. If the augmented matrix has no solution, then b is NOT a linear combination of the vectors.
For this example, b CAN be written as a linear combination.
Course website:
Linear Algebra Example Problems - Subspace Example #1
Linear Algebra Example Problems - Vector Space Basis Example #1
Linear Algebra Example: Span Questions
Linear Algebra Example Problems - Spanning Vectors #1
Linear Algebra Example Problems - Finding 'A' of a Linear Transformation #1
Linear Algebra Example Problems - Linear Combination of Vectors #2
Linear Algebra 7 | Examples for Subspaces
linear algebra vector space (25 examples)
Linear Algebra: number systems, overview of matrix math, 8-19-24
Linear Algebra Example Problems - Coordinate System Representation Example #1
Linear Algebra Example Problems - Spanning Vectors #2
Linear Algebra Example Problems - Diagonalizing a Matrix
Linear Algebra Example Problems - Linear Transformation Ax #1
Linear Transformations , Example 1, Part 1 of 2
Linear Algebra Example Problems - Change of Coordinates Matrix #1
Linear Algebra Example Problems - Onto Linear Transformations
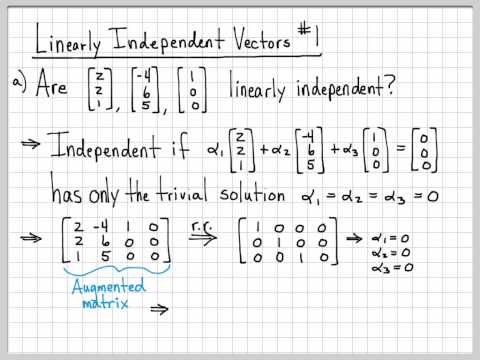
Linear Algebra Example Problems - Linearly Independent Vectors #1
Linear Algebra Example Problems - Linear Combination of Vectors #1
Gilbert Strang: Linear Algebra vs Calculus
Linear Algebra Example Problems - Eigenvalue Computation #1
Linear Algebra Example Problems - Subspace Example #2
Linear Algebra Example Problems - Finding 'A' of a Linear Transformation #2
Linear Algebra Example Problems - Subspace Example #4
Linear Algebra Example Problems - A Polynomial Subspace
Комментарии
 0:04:48
0:04:48
 0:04:47
0:04:47
 0:12:47
0:12:47
 0:04:31
0:04:31
 0:05:52
0:05:52
 0:03:53
0:03:53
 0:10:56
0:10:56
 0:30:16
0:30:16
 0:46:13
0:46:13
 0:05:54
0:05:54
 0:04:27
0:04:27
 0:04:41
0:04:41
 0:04:42
0:04:42
 0:09:06
0:09:06
 0:08:41
0:08:41
 0:05:20
0:05:20
 0:04:58
0:04:58
 0:03:37
0:03:37
 0:02:14
0:02:14
 0:04:13
0:04:13
 0:07:14
0:07:14
 0:07:40
0:07:40
 0:09:10
0:09:10
 0:06:14
0:06:14