filmov
tv
Olympiad Question: Solve this System of Equations | Step-by-Step Tutorial
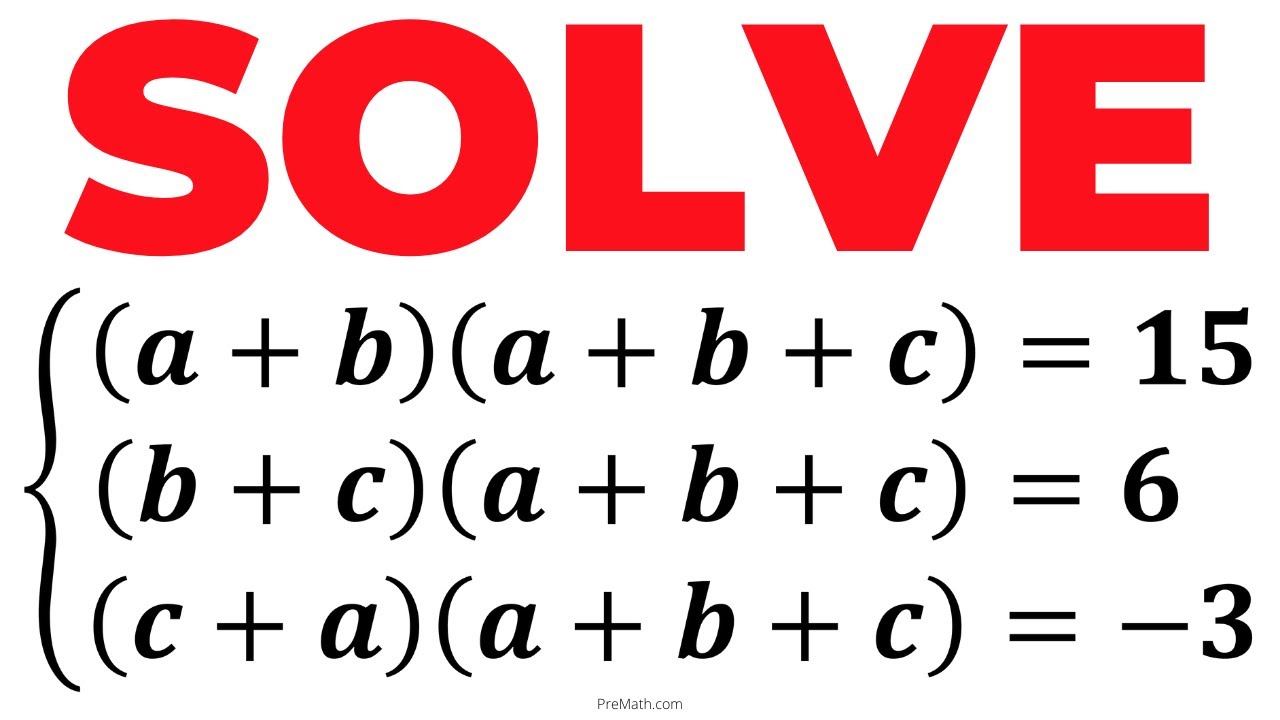
Показать описание
#OlympiadMathematics #OlympiadPreparation #CollegeEntranceExam
Olympiad Question: Solve this System of Equations | Step-by-Step Tutorial
Olympiad Question! Solve this System of Equations if X, Y, & Z are Integers | Step-by-Step Tutor...
Math Olympiad Question | You should know this trick!!
Norway Math Olympiad Question | You should be able to solve this!
A Nice Olympiad Exponential Multiplication Problem #short #olympiad #mathematics #maths #exponents
Math Olympiad Question | Learn How to Solve the System of Equations Fast | Math Olympiad Preparation
Luxembourg - Math Olympiad Question | You should know this trick
Olympiad Question. Can You Solve this? | Simple & In-Depth Explanation
Problem 66 : How to solve the most difficult Olympiad math question . 𝑰𝒇 𝒂^𝒃−𝒃=𝟐𝟏 a and b are??...
Math Olympiad Question | Equation solving | You should learn this trick to pass the exam
Olympiad Mathematics | Learn how to solve the system for x+y quickly | Math Olympiad Training
Olympiad Mathematics | Learn how to solve the system for X, Y and Z quickly | Math Olympiad Training
Olympiad Math Question! | Solve The System Equation for x, y and z
Math Olympiad Question | Solving System of Equations | Find X, Y, Z | Can you solve it?
Mathematical Olympiad | Solve system of Exponential Equations | Math Olympiad Training
Olympiad Mathematics | Solve a System of Equations the Easy Way
Olympiad Mathematics | Learn How to Solve the System of Equations Fast | Math Olympiad Preparation
Can You Solve this Math Olympiad Question? | System of Equations
Olympiad Mathematics | Learn How to Solve the System of Equations Fast | Math Olympiad Preparation
Germany | Can You Solve this? | A Nice Math Olympiad Problem (x,y) =? | 👇
Math Olympiad 3^m–2^m=65 | Math Olympiad Problems | Algebra
Russia | Math Olympiad Question | You should know this trick!!
Nice Algebra Question | Math Olympiad Problem | Let's solve this system of equations!
Olympiad Question | Two Methods to Solve System of Exponential Equations | Math Olympiad Training
Комментарии
 0:09:57
0:09:57
 0:08:32
0:08:32
 0:00:33
0:00:33
 0:03:21
0:03:21
 0:00:52
0:00:52
 0:09:13
0:09:13
 0:02:51
0:02:51
 0:08:43
0:08:43
 0:04:18
0:04:18
 0:01:54
0:01:54
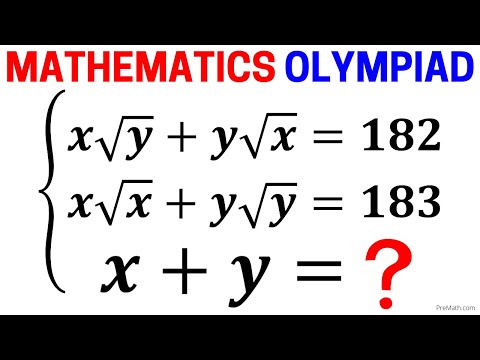 0:08:36
0:08:36
 0:08:08
0:08:08
 0:08:52
0:08:52
 0:04:19
0:04:19
 0:08:30
0:08:30
 0:05:22
0:05:22
 0:06:26
0:06:26
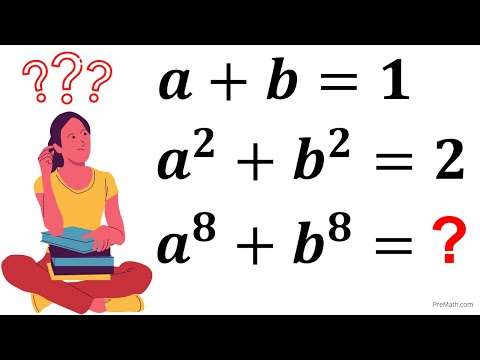 0:08:42
0:08:42
 0:05:36
0:05:36
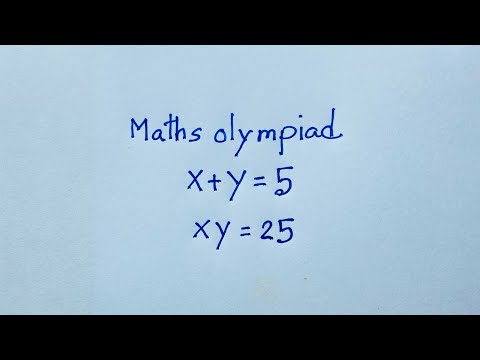 0:10:20
0:10:20
 0:10:49
0:10:49
 0:08:01
0:08:01
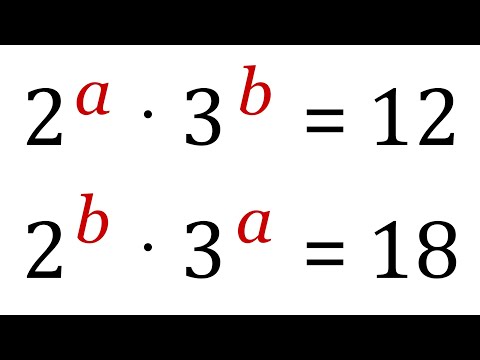 0:08:17
0:08:17
 0:10:42
0:10:42