filmov
tv
Olympiad Question. Can You Solve this? | Simple & In-Depth Explanation
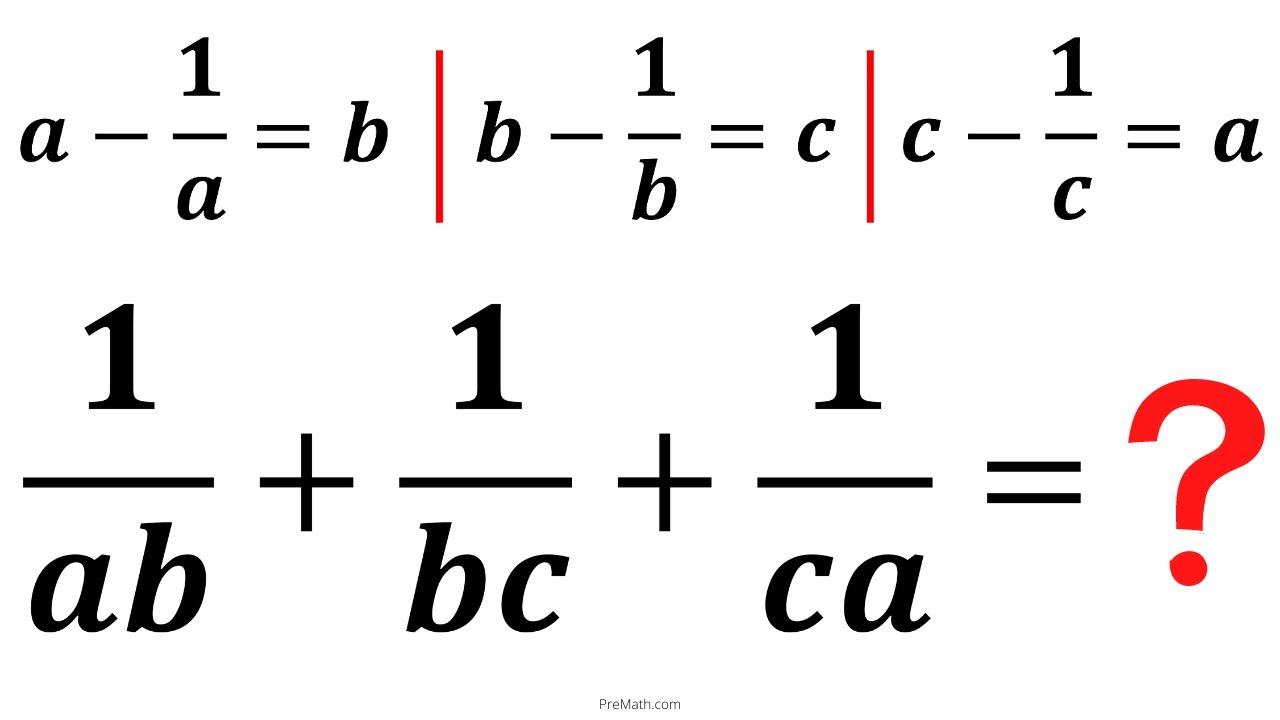
Показать описание
#OlympiadMathematics #OlympiadPreparation #CollegeEntranceExam
Can you solve this? | Olympiad Math Question
Norway Math Olympiad Question | You should be able to solve this!
Luxembourg - Math Olympiad Question | You should know this trick
Math Olympiad Question | Equation solving | You should learn this trick to pass the exam
A Nice Olympiad Exponential Multiplication Problem #short #olympiad #mathematics #maths #exponents
A Nice Math Olympiad Exponential Equation 3^x = X^9
A beautiful international math olympiad problem
France - Math Olympiad Question | An Algebraic Expression | You should be able to solve this!
Mexico - A Nice Math Olympiad Exponential Problem
Can you solve this Olympiad question??
Russia | Math Olympiad Question | You should know this trick!!
Math Olympiad Question | You should know how to solve this!!
The unexpectedly hard windmill question (2011 IMO, Q2)
Math Olympiad Question | Can You Solve This?
Math Olympiad 3^m–2^m=65 | Math Olympiad Problems | Algebra
Can you solve this Olympiad question??
Math Olympiad Question | Nice Algebra Equation | You should know this trick!!
Can you find Perimeter and Area of the right triangle? | (Solve) | #math #maths | #geometry
Germany | Math Olympiad Questions | can you solve this?
Can you solve this Olympiad question??
UK - Math Olympiad Question | You should be able to solve this without calculators!!
Can you solve this maths olympiad question?
Can you solve this Olympiad question??
Can you solve this Korean Maths Olympiad Problem 😳 Maths Challenge 📢 #ytshorts #byju #challenge...
Комментарии
 0:16:12
0:16:12
 0:03:21
0:03:21
 0:02:51
0:02:51
 0:01:54
0:01:54
 0:00:52
0:00:52
 0:02:34
0:02:34
 0:01:00
0:01:00
 0:08:40
0:08:40
 0:08:36
0:08:36
 0:05:09
0:05:09
 0:08:01
0:08:01
 0:02:24
0:02:24
 0:16:03
0:16:03
 0:03:28
0:03:28
 0:10:49
0:10:49
 0:10:34
0:10:34
 0:07:26
0:07:26
 0:09:58
0:09:58
 0:04:52
0:04:52
 0:08:02
0:08:02
 0:03:20
0:03:20
 0:01:58
0:01:58
 0:08:05
0:08:05
 0:00:50
0:00:50