filmov
tv
Solving A Functional Equation | Substitution
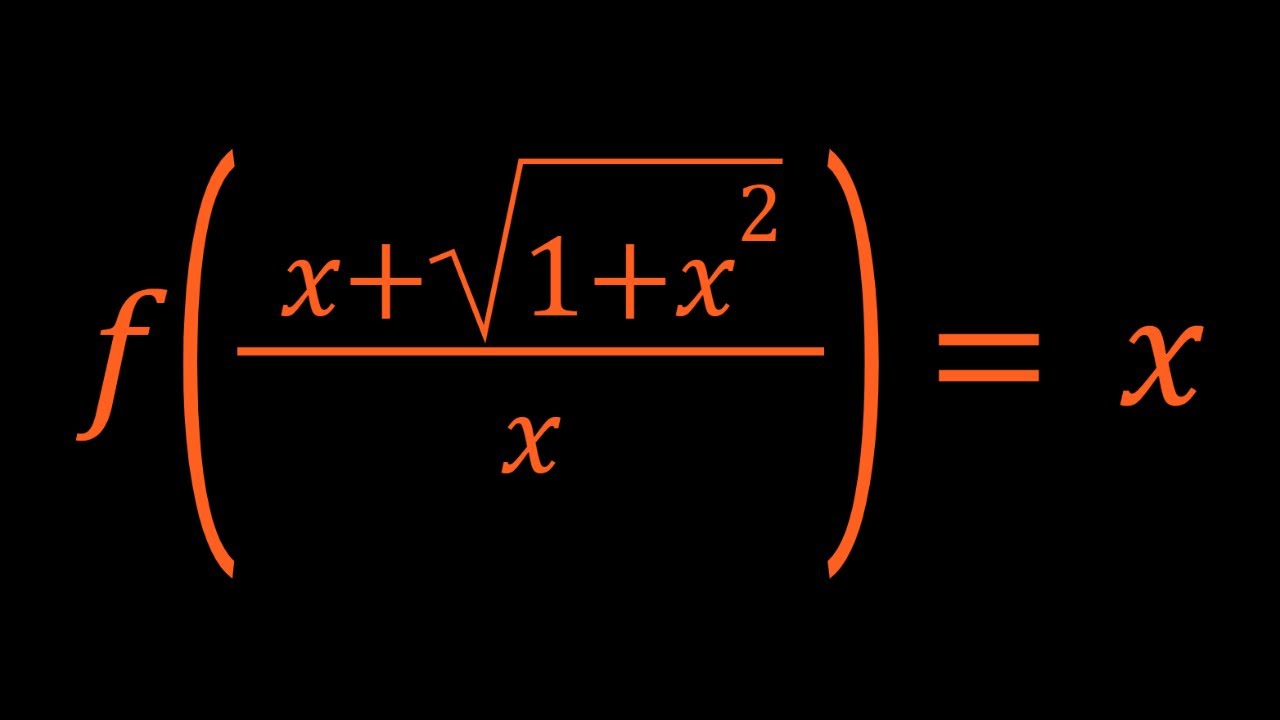
Показать описание
🤩 Hello everyone, I'm very excited to bring you a new channel (SyberMath Shorts).
Enjoy...and thank you for your support!!! 🧡🥰🎉🥳🧡
If you need to post a picture of your solution or idea:
#functionalequations #functions #function
via @YouTube @Apple @Desmos @NotabilityApp @googledocs @canva
PLAYLISTS 🎵 :
Enjoy...and thank you for your support!!! 🧡🥰🎉🥳🧡
If you need to post a picture of your solution or idea:
#functionalequations #functions #function
via @YouTube @Apple @Desmos @NotabilityApp @googledocs @canva
PLAYLISTS 🎵 :
Methods of Functional Equations
A Super Quick and Easy Functional Equation
Huh? How do you solve this? Functional equation for precalculus students
Learn Functions – Understand In 7 Minutes
How To Solve A Functional Equation | The Easy Way
Functional Equation
Solving a Quick and Easy Functional Equation
Solving a Functional Equation
Oxford Interview Question: Functional Equation
Solving a Quick and Easy Functional Equation
A Nice and Easy Functional Equation
Let's Solve A Functional Equation | 2nd Method?
Composite Functions
Solving a Homemade Functional Equation 1
Let's Solve A Functional Equation #mathematics #function #algebra
Solving a Functional Equation
Solving A Functional Equation #maths #mathematics #algebra #exponential #mathtube
A Functional Equation from Samara Math Olympiads
Solving A Functional Equation | Substitution
Solving A Functional Equation
Gaining Insights: Solving a Functional Equation
Solving a Functional Equation | f(x)+f(x-1)=x^2
Destroying A Functional Equation Via Substitution
Solving A Nice Functional Equation
Комментарии
 0:07:40
0:07:40
 0:06:49
0:06:49
 0:05:46
0:05:46
 0:09:43
0:09:43
 0:07:19
0:07:19
 0:14:15
0:14:15
 0:05:47
0:05:47
 0:10:36
0:10:36
 0:05:50
0:05:50
 0:06:19
0:06:19
 0:05:07
0:05:07
 0:08:53
0:08:53
 0:05:23
0:05:23
 0:08:55
0:08:55
 0:00:36
0:00:36
 0:10:36
0:10:36
 0:00:53
0:00:53
 0:08:47
0:08:47
 0:08:28
0:08:28
 0:12:35
0:12:35
 0:10:22
0:10:22
 0:08:59
0:08:59
 0:00:42
0:00:42
 0:09:50
0:09:50