filmov
tv
Huh? How do you solve this? Functional equation for precalculus students
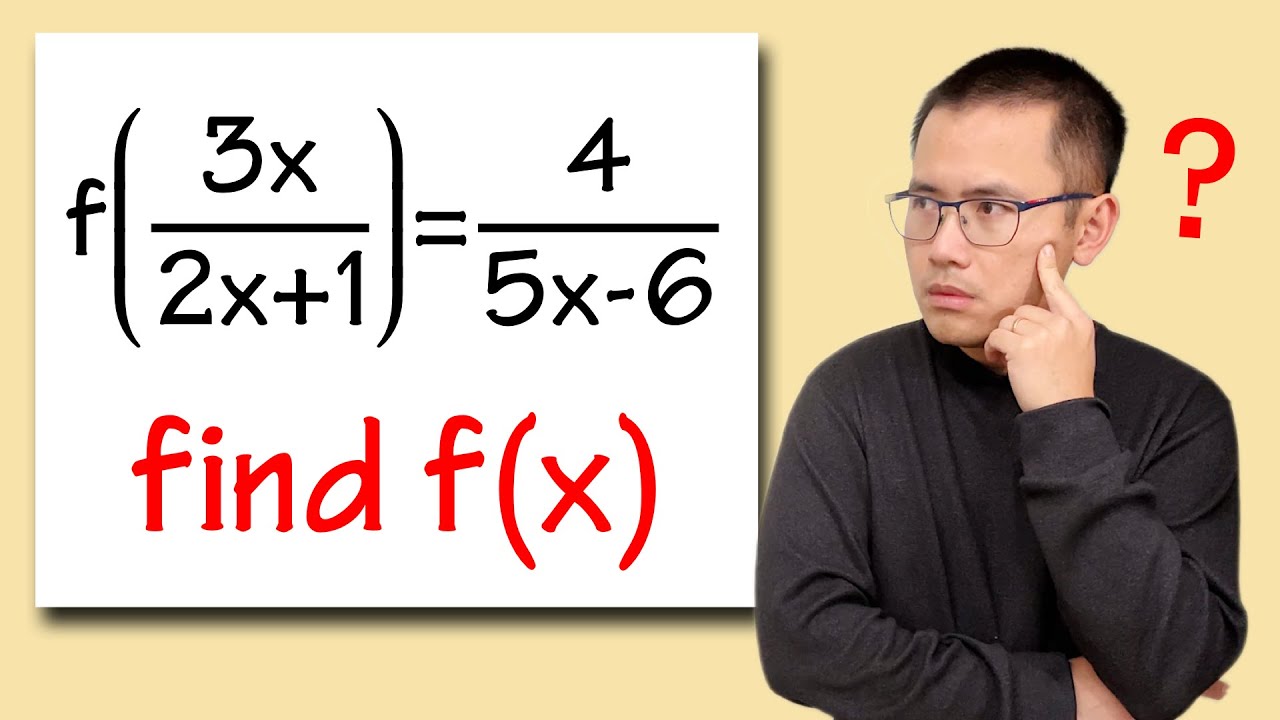
Показать описание
Learn how to solve a function equation based on an inverse function for your precalculus class. We will see how to solve for f(x) if f(3x/(2x+1))=4/(5x-6). We will cover how to find the inverse of a rational function and how to simplify complex fractions.
-----------------------------
-----------------------------
#math #algebra #mathbasics
-----------------------------
-----------------------------
#math #algebra #mathbasics
Huh? How do you solve this? Functional equation for precalculus students
Bad Girl vs Good Girl At School! How to Become POPULAR at School
Huh?? #knowledge #maths #satmath #satexam #what #question
From Poor Doll To Rich Doll Makeover ❤️ *Best Barbie Gadgets and Crafts by YayTime! STAR
SRPUNKI KISS EDITION, but PINKI Falls in LOVE with BLACK?! Incredibox Sprunki Animation
Classmates Bully a Poor Girl, But Unexpectedly, Years After Her Death, She Returns for Revenge!
Car Dies While Driving Huh? 🔧👀 SMH😑 #shorts #tevideos #honda #mechanic
From Nerd to LadyBug ❤️ Extreme Beauty Makeover in Jail
Brain out 'Crazy find' level 44 solution / huh, where did the fish go / #viral #trending #...
Can you solve it? Huh! I can't believe! Prove it in comment!
I GOT INTO A FIGHT WITH MY TWIN BROTHER..
CEO Save A Girl By Blood Transfusion At Hospital! Not Realizing It's Child Of His ONS 7 Years A...
Huh? Can you solve it?
HUH No one can solve it ?? | Mrbeast can solve this with #elonmusk and #foryou
🔥Delivery guy mocked by everyone turns out to be a hidden billionaire powerhouse, Shocking everyone!...
Points, lines, planes, etc. - June Huh
Sprunki fans can't solve the equation😱The answer is in the comment!
Huh #funny #retable #ytshorts #gettingolder #90slove #trendingshorts #new #rubikscube
huh
Huh??? #maths #satmathhacks #funnyjokes #knowledge #satmath #exam
huh this is impossible to solve
HUH: part 4
😲Brain twisters that will make you say 'huh?'🤔#Shorts #Fun
Hmm 🧐 huh 🤔 maths puzzle 🧩 easy but confusing ||#youtubeshorts #shorts#confusing #huh#hmm #puzzle...
Комментарии
 0:05:46
0:05:46
 0:20:46
0:20:46
 0:00:58
0:00:58
 3:00:50
3:00:50
 0:17:40
0:17:40
 2:36:24
2:36:24
 0:00:16
0:00:16
 0:25:24
0:25:24
 0:00:11
0:00:11
 0:00:19
0:00:19
 0:10:10
0:10:10
 2:06:28
2:06:28
 0:00:26
0:00:26
 0:00:06
0:00:06
 2:25:03
2:25:03
 0:16:11
0:16:11
 0:00:11
0:00:11
 0:00:17
0:00:17
 0:00:16
0:00:16
 0:01:01
0:01:01
 0:00:07
0:00:07
 0:00:20
0:00:20
 0:00:31
0:00:31
 0:00:09
0:00:09