Solving a Radical Functional Equation in Two Ways

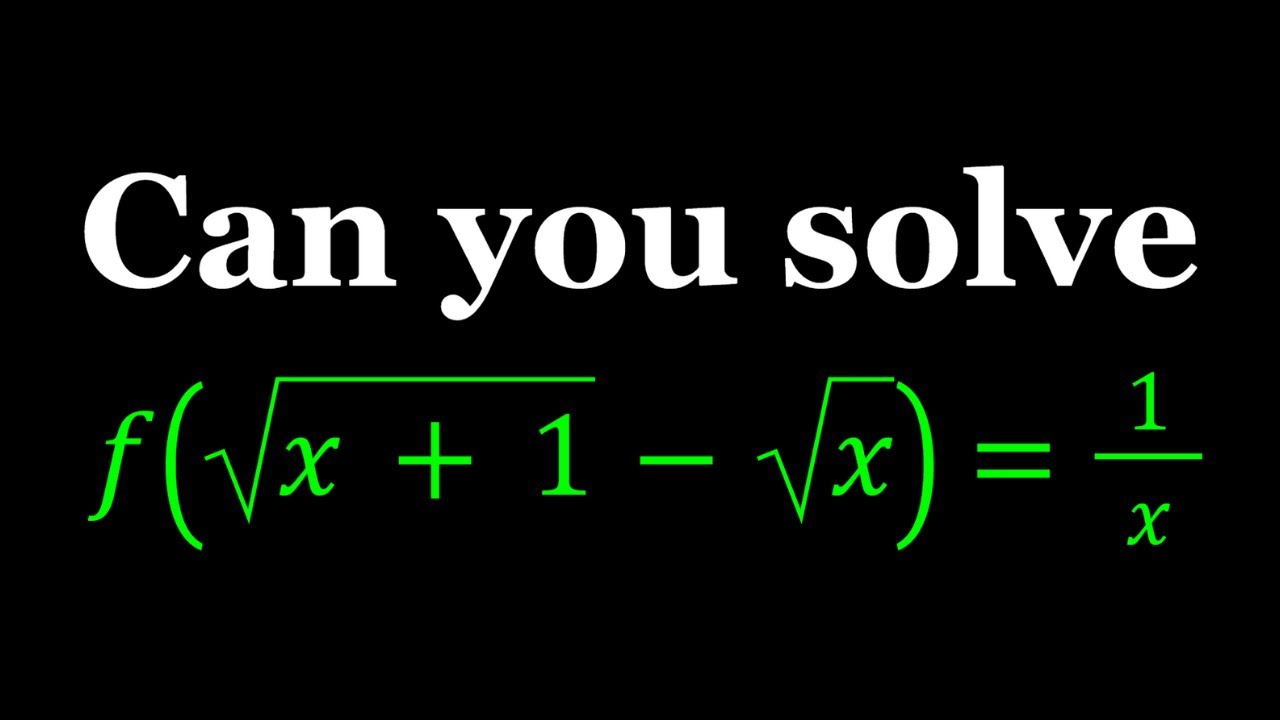
Показать описание

If you need to post a picture of your solution or idea:
#ChallengingMathProblems #FunctionalEquations

PLAYLISTS 🎵 :

Рекомендации по теме

Комментарии

We consider the equation
√( x + 1 ) - √x = t
where 0 < t < 1. Setting
a := √x,
b := √( x + 1 ),
we have
a^2 = x,
b^2 = x + 1.
Then we have
b - a = t　…①
b^2 - a^2 = 1　…②
② is equivalent to
( b - a )( a + b ) = 1
t( a + b ) = 1
a + b = 1/t　…③
③ - ① implies that
2a = 1/t - t
√x = ( 1/2 )( 1/t - t )
x = ( 1/4 )( 1/t - t )^2
Hence we obtain f( t ) = 4/( 1/t - t )^2 or f( t ) = 4t^2/( 1 - t^2 )^2.

f( √( x + 1 ) - √x ) = 1/x
Assume that f is continuous on [ 0, 1 ). Letting x → ∞ we see that f( 0 ) = 0.

dlnkbfv

Awesome video.
Idea:
Rationalize the denominator in
1/(7^1/4 + 5^1/3 + 3^1/2)

akssumusic

Yet again a valuable video, thanks! :)

PenandPaperScience

(1/t)=√(x+1)+√x, so t-(1/t)=-2√x squaring both sides etc

devadasb

It can also be solved with the hyperbolic substitution x=(sinht)^2 followed by u=e^(-t)

calculer

By inspection one should realize by taking sort of x to RHS and squaring the x term cancels right away. So method 1 is the best in this case.
However if the two radicals are sort x and sqrt(1-x) it’s prudent to square as is coz x and -x cancels out right away. Those rules I follow all the time to keep the simplification simple.

ManjulaMathew-wbzn

It can also be expressed as f(x)= [2x/(x^2-1)]^2. Notice that f(x) is undefined for x=-1 as well as x=1.

Blaqjaqshellaq

3:25 i wasn't looking at the screen when you said 4t² and it sounded like 40²

ahmadmazbouh

I definitely started out by trying what you call Method 2 first, got to the (a+b+c)² part, and realized there must be a simpler way. I found it; your Method 1 :)

txikitofandango

Third method: sqr(x+1) - sqr(x) = t and sqr(x+1) + sqr(x) = u, Soon, t * u =1 or u = 1/t, Substituting into the second equation, we get: sqr(x+1) + sqr(x) = 1/t. Now, just add the 2 equations and square, to determine the value of x.

eronmagnoaguiaresilva

Let g : (0, ♾) —> (0, 1) such that g(x) = sqrt(x + 1) – sqrt(x) and let h : (0, ♾) —> (0, ♾) such that h(x) = 1/x. We want to find all f : (0, 1) —> (0, ♾) such that f°g = h. To do this, we should try to check if g is right-invertible. We want there to be some φ : (0, 1) —> (0, ♾) such that g°φ = id : (0, 1) —> (0, 1), which means g[φ(x)] = x. Hence sqrt[φ(x) + 1] – sqrt[φ(x)] = x. Notice that there exists no φ(x) such that sqrt[φ(x) + 1] + sqrt[φ(x)] = 0, hence sqrt[φ(x) + 1] – sqrt[φ(x)] = x is equivalent to 1 = x·(sqrt[φ(x) + 1] + sqrt[φ(x)]), which is equivalent to sqrt[φ(x + 1) + 1] + sqrt[φ(x)] = 1/x. Therefore, 1/x – x = 2·sqrt[φ(x)], hence φ(x) = (1/x – x)^2/4 = (1/x^2 – 2 + x^2)/4 = x^2/4 – 1/2 + 1/(4·x^2). Therefore, φ(x) + 1 = x^2/2 + 1/2 + 1/(2·x^2) = (1/x^2 + 2 + x^2)/4 = (1/x + x)^2/4, so sqrt[φ(x) + 1] = (1/x + x)/2, hence g[φ(x)] = x indeed. As such, we have proven the existence and uniqueness of φ. What remains is that f°g = h implies (f°g)°φ = f°(g°φ) = f°id = f = h°φ. This means f(x) = 1/[x^2/4 – 1/2 + 1/(4·x^2)] = 4·x^2/(x^4 – 2·x^2 + 1) = (2·x)^2/(x^2 – 1)^2 = [2·x/(x^2 – 1)]^2.

angelmendez-rivera