filmov
tv
[Algebra] Is there any cubic formula?

Показать описание
In yesterday's video, we tried to solve an inequality of rational functions (functions in fraction form for both numerator the top part and denominator the bottom part being polynomials) but ended up with one of the factors a cubic polynomial that was not factorable with integer coefficients. It led us to the following question: is there any way that we can solve such a cubic polynomial?
In math class, we learn that for any quadratic equation, there exists a general solution called the quadratic formula; today, we are trying to figure out a general solution for an arbitrary cubic equation, a.k.a. the cubic formula, by using Cardano's method.
The remaining derivation of the cubic formula is in the next video:
In math class, we learn that for any quadratic equation, there exists a general solution called the quadratic formula; today, we are trying to figure out a general solution for an arbitrary cubic equation, a.k.a. the cubic formula, by using Cardano's method.
The remaining derivation of the cubic formula is in the next video:
[Algebra] Is there any cubic formula?
500 years of NOT teaching THE CUBIC FORMULA. What is it they think you can't handle?
Solving a cubic equation
Solving a cubic equation in two ways. A challenge in algebra.
Solving a Cubic equation Using an Algebraic Trick
Factoring a cubic polynomial
Solving A Nice Cubic Equation | #Factoring #Algebra
Solving a cubic system
2013—2015 past papers | MAT livestream 2024
Solving A Cubic System #algebra #polynomials
How to Solve Advanced Cubic Equations: Step-by-Step Tutorial
Solving a Cubic Polynomial in Two Ways
He can factor a cubic trinomial
[Algebra] Find out the remaining solution of general cubic equation with high school algebra 🤣
Solving a cubic equation with “only one” solution
Solving a cubic equation with a parameter
Solving a cubic equation and looking for integer solutions. Substitution rules.
Factorise Cubic Equation Grade 12: Introduction
Cubic Formula Derivation
A Cubic Equation | x^3+x^2=1/8
ALGEBRAIC EXPRESSIONS: Cubic Polynomial
Simple way to solve a cubic equation
Factor and Solve Cubic Equations in Less Than One Minute! - Super Simple Trick
Solving a cubic equation with irrational coefficients. A radical challenge in algebra.
Комментарии
![[Algebra] Is there](https://i.ytimg.com/vi/QiO7JucVZEs/hqdefault.jpg) 0:23:44
0:23:44
 0:36:58
0:36:58
 0:07:26
0:07:26
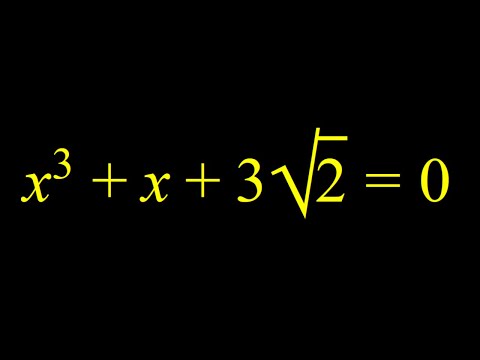 0:14:44
0:14:44
 0:11:45
0:11:45
 0:06:30
0:06:30
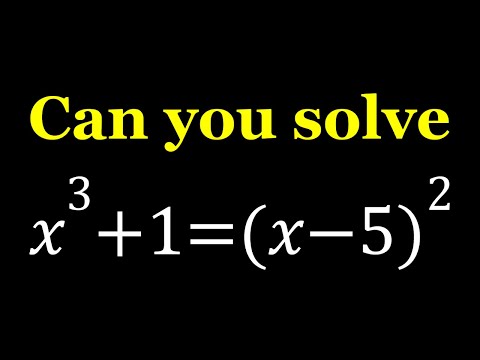 0:09:20
0:09:20
 0:14:14
0:14:14
 2:02:47
2:02:47
 0:08:41
0:08:41
 0:10:52
0:10:52
 0:09:55
0:09:55
 0:00:14
0:00:14
![[Algebra] Find out](https://i.ytimg.com/vi/xhjNRQxqJTM/hqdefault.jpg) 0:39:32
0:39:32
 0:05:17
0:05:17
 0:11:43
0:11:43
 0:08:46
0:08:46
 0:06:17
0:06:17
 0:00:18
0:00:18
 0:10:27
0:10:27
 0:05:07
0:05:07
 0:04:56
0:04:56
 0:07:18
0:07:18
 0:06:36
0:06:36