filmov
tv
Solving a cubic equation and looking for integer solutions. Substitution rules.
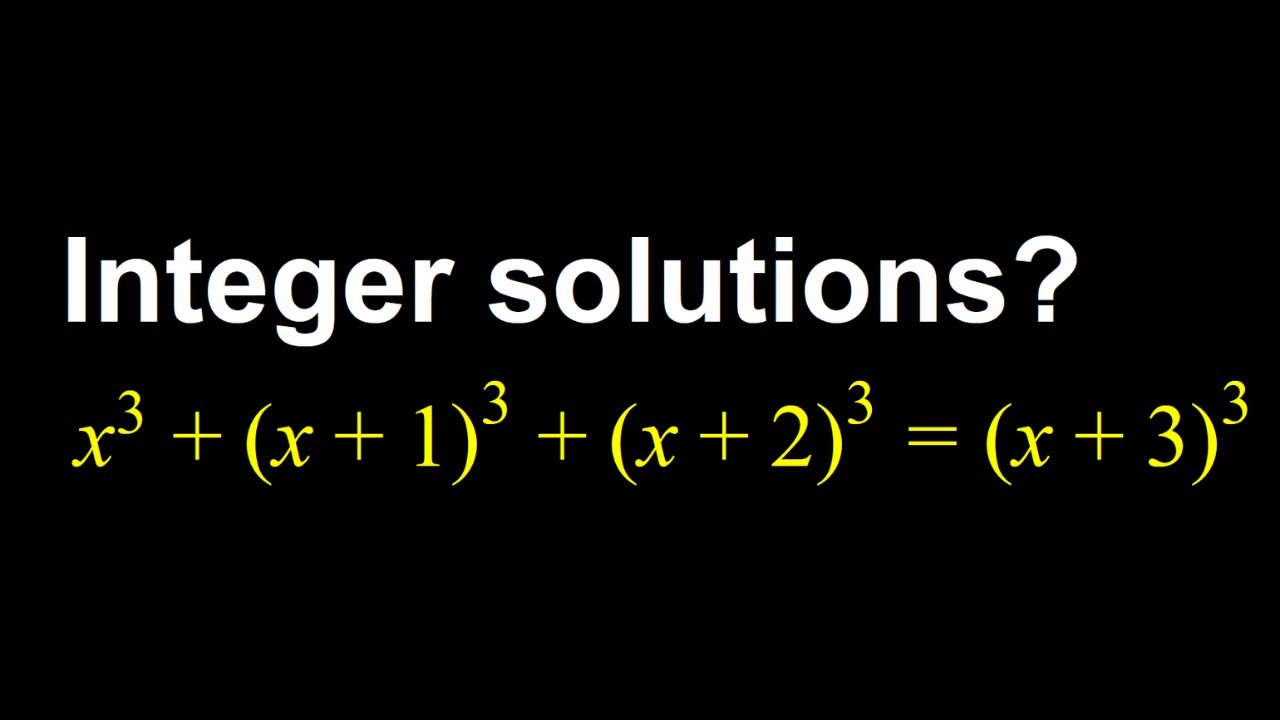
Показать описание
This video is about a cubic equation that can be solved without using the cubic formula.
Polynomial expressions,sum of cubes,algebra,algebraic equations,SyberMath,algebraic manipulations,substitution,Challenging Math Problems,Non-routine Math Problems,polynomial equations,an algebra challenge,algebraic identities,non-standard methods,symmetry,math,maths,mathematics,An algebraic challenge,Polynomial equations,an equation,cubic equations,A cubic equation that can be solved easily,power of substitution,integer solutions,diophantine equations
Polynomial expressions,sum of cubes,algebra,algebraic equations,SyberMath,algebraic manipulations,substitution,Challenging Math Problems,Non-routine Math Problems,polynomial equations,an algebra challenge,algebraic identities,non-standard methods,symmetry,math,maths,mathematics,An algebraic challenge,Polynomial equations,an equation,cubic equations,A cubic equation that can be solved easily,power of substitution,integer solutions,diophantine equations
Simple way to solve a cubic equation
How to Solve Advanced Cubic Equations: Step-by-Step Tutorial
500 years of NOT teaching THE CUBIC FORMULA. What is it they think you can't handle?
CUBIC EQUATION FACTORIZATION SHORTCUT/ SOLVING CUBIC EQUATIONS IN 10 SECONDS/ Math Tricks.
Factor and Solve Cubic Equations in Less Than One Minute! - Super Simple Trick
Solving Cubic Equations (factoring)
Solving a Cubic equation Using an Algebraic Trick
solving a cubic equation by completing the cube
12 th maths quarterly exam 2024 question paper and important questions
Solving Simple Cubic Equations
Factorise Cubic Equation Grade 12: Introduction
How to Solve Advanced Cubic Equations: Easy-to-Understand Explanation
Solve any Cubic Equations | Cardano's Method |
Solving a simple cubic equation. A trick you should know!
How To Solve Cubic Equations
Find Factors and Solve Cubic Equations in Less Than ONE Minute! - Leading Coefficient Is Not One
Solve Cubic Equations - Total Sum Method
How to prove the cubic formula (from scratch)
How to Solve a Rubik’s Cube in 4 Moves
Solve Cubic Equations - Synthetic Division Method
Solving Polynomial Equations By Factoring and Using Synthetic Division
Can You Solve this Cubic Equation in 1 Minute? | Quick & Simple Explanation
Factorising cubic functions: The kx method
Classwiz How-To: Solving a Cubic Equation
Комментарии
 0:04:56
0:04:56
 0:10:52
0:10:52
 0:36:58
0:36:58
 0:12:06
0:12:06
 0:07:18
0:07:18
 0:03:32
0:03:32
 0:11:45
0:11:45
 0:07:28
0:07:28
 0:05:02
0:05:02
 0:09:13
0:09:13
 0:06:17
0:06:17
 0:11:25
0:11:25
 0:04:20
0:04:20
 0:06:41
0:06:41
 0:09:29
0:09:29
 0:09:10
0:09:10
 0:09:51
0:09:51
 0:40:16
0:40:16
 0:01:15
0:01:15
 0:09:30
0:09:30
 0:14:19
0:14:19
 0:02:52
0:02:52
 0:10:22
0:10:22
 0:03:14
0:03:14