filmov
tv
Proof that f(x) = x^2 is Uniformly Continuous on (0, 1)
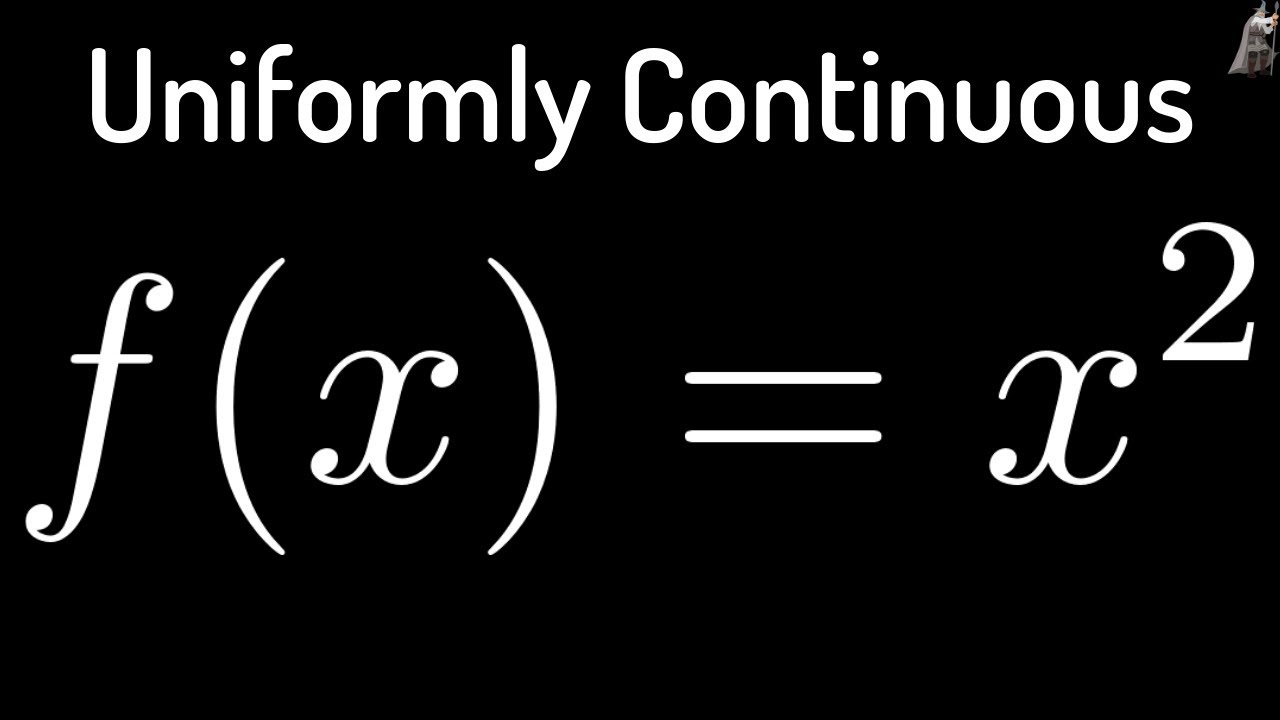
Показать описание
Proof that f(x) = x^2 is Uniformly Continuous on (0, 1)
Proof that f(x) = x^2 is Uniformly Continuous on (0, 1)
proving x^2 is continuous using the epsilon delta definition
Proof: f(x) = |x| is Continuous using Epsilon Delta Definition | Real Analysis Exercises
Proof: f(x) = x is Continuous using Epsilon Delta Definition | Real Analysis Exercises
Show that `f(x) =x^(2)` is continuous at x=2 lt
Injective Functions | Is f(x)=x^2 Injective? | A formal proof | Analysis | Math2Go
Proof of a Limit Value Using Epsilon and Delta
Proof that f(x) = x*|x| is Differentiable at x = 0
Prove that f∶[0,1]→R defined by f(x)=x^2 is uniformly continuous.
Proving the Function f(x) = sqrt(x + 2) is One to One(Injective) using the Definition
Show that f(x) is continuous at x=4
Proof that f(x) = 1/x is Continuous on (0, infinity) using Delta-Epsilon
Show that the function f(x)=|x-2| is continuous but not differentiable at x=2.
Determine if the Function f(x, y)= x^2 - y^2 is a Harmonic Function
How to Prove the Rational Function f(x) = 1/(x - 2) is Surjective(Onto) using the Definition
How REAL Men Integrate Functions
[Proof] Function is bijective
Show that ` f(x)= x^2 ` is differentiable at x=1 and find f'(1),
Prove that the function f(x) = 1/x^2 is uniformly continous on [a, infinity)
This is a very famous limit
How to Prove a Function is Injective(one-to-one) Using the Definition
#26 || Problem#6 || show that [𝝏/𝝏𝒙 |𝒇(𝒛)|]^𝟐+[𝝏/𝝏𝒚 |𝒇(𝒛)|]^𝟐=|𝒇^′ (𝒛)|^𝟐 || 18MAT41||...
show that the function `(i) f : N to N : f (x) =x^(2)` is one-one into (ii) `f : Z to Z :
5 simple unsolvable equations
Комментарии
 0:03:34
0:03:34
 0:09:35
0:09:35
 0:04:19
0:04:19
 0:04:46
0:04:46
 0:02:01
0:02:01
 0:04:44
0:04:44
 0:09:17
0:09:17
 0:02:50
0:02:50
![Prove that f∶[0,1]→R](https://i.ytimg.com/vi/uUs5OsxI2mQ/hqdefault.jpg) 0:22:44
0:22:44
 0:02:14
0:02:14
 0:01:51
0:01:51
 0:09:56
0:09:56
 0:04:08
0:04:08
 0:02:00
0:02:00
 0:06:03
0:06:03
 0:00:35
0:00:35
![[Proof] Function is](https://i.ytimg.com/vi/oTub-N4uopw/hqdefault.jpg) 0:08:50
0:08:50
 0:05:52
0:05:52
 0:13:57
0:13:57
 0:00:48
0:00:48
 0:03:35
0:03:35
 0:16:13
0:16:13
 0:03:13
0:03:13
 0:00:50
0:00:50