Proof f(x)=sin(x) is Continuous using Epsilon Delta Definition | Real Analysis Exercises

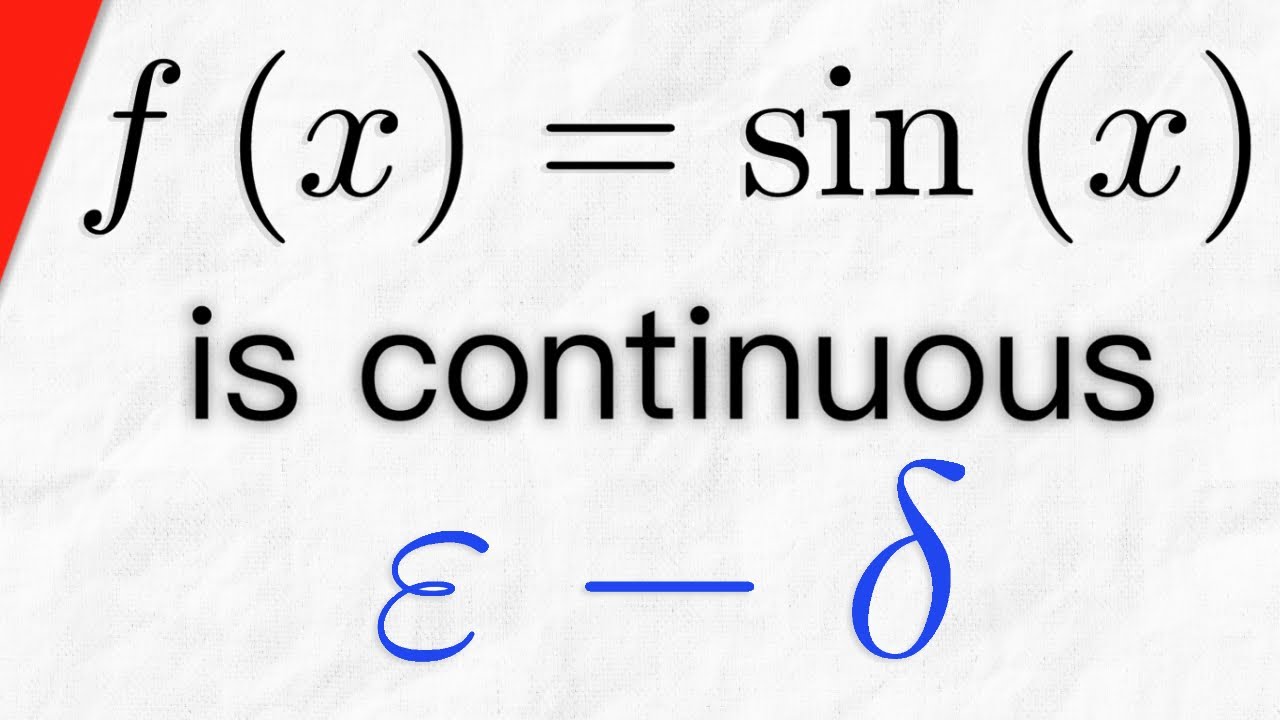
Показать описание

We prove that f(x)=sin x, the sine function, is continuous on its entire domain - the real numbers. We complete this proof using the epsilon delta definition of continuity of a function at a point. To do this, we simply take an epsilon greater than 0 and an arbitrary point c from our domain, then go through the motions of finding a delta greater than 0 so that any x in D that is within delta of c has an image within epsilon of c's image. This will be surprisingly easy so long as we remember a few important trigonometric identities/inequalities! Let me know if there are more epsilon delta continuity proofs you want to see!

#RealAnalysis #Math

★DONATE★

Thanks to Robert Rennie, Barbara Sharrock, and Rolf Waefler for their generous support on Patreon!

Follow Wrath of Math on...

Рекомендации по теме

Комментарии

Also can be proved by limit and diffrentiation concepts. If the function is diffrentiable, then it is continous by defination. So, we can use [f(x+h)-f(x)]/h formula to prove that easily. I dont know these delta function and all as I am grade 12 student, but if I was asked to prove that, I would use this approach. Sry for my english

maheshpatel

Another way to do this, but not as good, would be to take the arcsin to get the "x - c" term to pop out. I say it's not as good because it involves a little more work, and even when you're done (it turns out that delta = 2*arcsin(epsilon/2) ), it's fair to then start wondering whether arcsin has any weird behavior that makes it a bad solution. I mean, it looks like it should satisfy the requirements of the original problem since arcsin(0) = 0, but a person can feel a lot more comfortable that a simple "delta = epsilon" will scale things down to nothing as desired. You also have to account for periodicity; hardly insurmountable, but it's still a needless hassle.

I am sort of working on a mental Foolproof Guide To Epsilon-Delta; obviously nothing is foolproof here. But I feel like the first milestone to success is to find a way to pop out a term of |x - c|. Once you've done that, find a way to get rid of any remaining x's, probably by applying "this must be less than that" logic and possibly constraining delta as part of that logic. Once you've done that, unceremoniously shove everything other than the |x - c| to the other side, and then you're done. Maybe?

kingbeauregard

your sound like sheldon cooper of big bang theory.... plus great explanation ❤

codingnewbie

Great video. I might be nitpicky but |sin(x)|<=|x| seems very small angle approximation'ish to me but it's been awhile since i've seen the simple derivation for arc length = radius * subtended angle. Nice using triangles though. I usually like to think for the cosine one just in terms of bounds of the periodic graph of sine.

theproofessayist

Hey can you show us a really hard epsilon-delta? Like suppose the function is 1 / [(x+1)(x+2)(x+3)]; that's got to be super duper difficult to epsilon-delta into submission, right? Unless ... it's actually tons easier than it looks?

kingbeauregard

Since it is also true that |sin(x)|<=1, can you just set delta = 2?

adoxographer

Proof f(x)=sin(x) is Continuous using Epsilon Delta Definition | Real Analysis Exercises

Proof f(x)=sin(x) is Continuous using Epsilon Delta Definition | Real Analysis Exercises

prove that sinx is continuous function

f(x)=sin(x) is a Continuous Function

Proof: f(x) = x is Continuous using Epsilon Delta Definition | Real Analysis Exercises

Proof: f(x) = |x| is Continuous using Epsilon Delta Definition | Real Analysis Exercises

Visualizing the derivative of sin(x)

Continuity | Continuous | sinx is continuous | Whether sinx is continuous for all values of x or not

f(x) = sin x is uniformly continuous on [0, ∞) |Real Analysis |Examples of uniform continuity

Integral calculus for Machine Learning | Mathematical foundations for ML

Example 19 - Show that f(x) = sin (x2) is continuous - Examples - Teachoo

Is the function defined by f(x) = x2 – sin x + 5 continuous at x = π?

Does Derivative Have to be Continuous? (feat. x^2sin(1/x))

Sine Curve and the Unit Circle

IIT Bombay CSE 😍 #shorts #iit #iitbombay

The Sine Function: f(x) = sin(x)

Epsilon Delta Continuity (Example 6): 1/x

Show that the function defined by `f(x) = sin(x^2)` is a continuous function....

f(x)=sin(x) is a Differentiable Function

Show that the function: f(x)= x^2 *sin(1/x) at x!=0 f(x)= 0 at x=0 is continuous at x=0 ?#shorts

show that sinx is continuous for every value of X

This is a very famous limit

When mathematicians get bored (ep1)

The function `f(x) =sin|x|` is continuous for all x

f(x)= sinx is continuous or not by graphical method #short