filmov
tv
A continuous function on a compact set has compact image, Real Analysis II

Показать описание
In this video, we prove that if a function f is continuous on a compact set K, then the image f(K) is also compact. We approach this proof in two ways: first by showing that f(K) is sequentially compact, and then by using the open cover definition of compactness.
For the sequential compactness proof, we take a sequence in f(K) and pull it back to K via the preimage, which yields a sequence in K. Since K is compact, we know this sequence has a convergent subsequence in K, and by continuity, its image in f(K) will also converge. This shows that f(K) is sequentially compact.
For the second proof using open covers, we start with an open cover of f(K), pull each open set back to create an open cover of K, and use the compactness of K to find a finite subcover. This finite subcover maps back to give a finite subcover of f(K), confirming the compactness of f(K).
These two proofs, while distinct, follow a similar logical structure and emphasize the core ideas of compactness, sequential compactness, and continuity.
#Mathematics #math #maths #Compactness #MetricSpaces #MathProof #RealAnalysis #STEM #CompactSets #Topology #advancedcalculus
For the sequential compactness proof, we take a sequence in f(K) and pull it back to K via the preimage, which yields a sequence in K. Since K is compact, we know this sequence has a convergent subsequence in K, and by continuity, its image in f(K) will also converge. This shows that f(K) is sequentially compact.
For the second proof using open covers, we start with an open cover of f(K), pull each open set back to create an open cover of K, and use the compactness of K to find a finite subcover. This finite subcover maps back to give a finite subcover of f(K), confirming the compactness of f(K).
These two proofs, while distinct, follow a similar logical structure and emphasize the core ideas of compactness, sequential compactness, and continuity.
#Mathematics #math #maths #Compactness #MetricSpaces #MathProof #RealAnalysis #STEM #CompactSets #Topology #advancedcalculus
3 Step Continuity Test, Discontinuity, Piecewise Functions & Limits | Calculus
Is the function continuous?
Continuous, Discontinuous, and Piecewise Functions
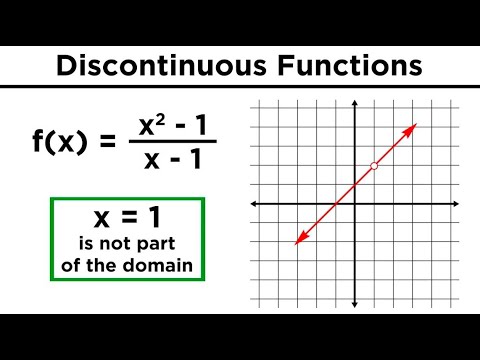
Is the function continuous or not
Real Analysis 27 | Continuity and Examples
Average Value of a Continuous Function on an Interval
Limit of a Function l What is a Continuous Function?
Defining a function at a point to make it continuous | Limits | Differential Calculus | Khan Academy
Continuous Function | Continuity of a Function 1
Find the values a and b that make the piecewise function continuous
Calculus - Introduction to Continuous and Discontinuous Functions | Don't Memorise
Continuity Basic Introduction, Point, Infinite, & Jump Discontinuity, Removable & Nonremovab...
Calculus - Continuous functions
Continuity and Differentiability EXPLAINED with Examples
What is continuity?
Continuity and Differentiability
Determine if the Piecewise Function is Continuous by using the Definition of Continuity
Real Analysis 29 | Combination of Continuous Functions
Composition of Continuous Functions is Continuous | Real Analysis
differentiable⟹continuous
Can A Function Be Continuous At Only One Point?
Continuous and Uniformly Continuous Functions
Continuous Function | Continuity of a Function 2
402.4A5 Continuous Functions and Open Sets
Комментарии
 0:10:10
0:10:10
 0:12:42
0:12:42
 0:05:18
0:05:18
 0:00:54
0:00:54
 0:09:59
0:09:59
 0:08:03
0:08:03
 0:07:23
0:07:23
 0:04:57
0:04:57
 0:08:38
0:08:38
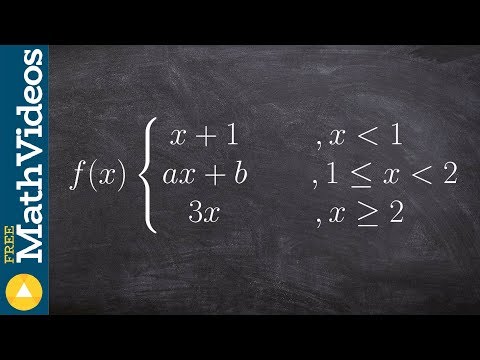 0:03:44
0:03:44
 0:05:43
0:05:43
 0:13:31
0:13:31
 0:08:45
0:08:45
 0:05:33
0:05:33
 0:04:32
0:04:32
 0:32:48
0:32:48
 0:04:01
0:04:01
 0:07:56
0:07:56
 0:04:53
0:04:53
 0:00:49
0:00:49
 0:14:21
0:14:21
 0:05:13
0:05:13
 0:12:15
0:12:15
 0:16:16
0:16:16