filmov
tv
Can You Prove the Triangle Inequality?

Показать описание
We prove the triangle inequality, |x+y| is less than or equal to |x| + |y|. This is a proof that is often shown in discrete math or real analysis.
#TriangleInequality #MathProof #discretemathematics
**Re-Upload with Fixed Audio**
Join this channel to get access to perks:
Hello, welcome to TheTrevTutor. I'm here to help you learn your college courses in an easy, efficient manner. If you like what you see, feel free to subscribe and follow me for updates. If you have any questions, leave them below. I try to answer as many questions as possible.
#TriangleInequality #MathProof #discretemathematics
**Re-Upload with Fixed Audio**
Join this channel to get access to perks:
Hello, welcome to TheTrevTutor. I'm here to help you learn your college courses in an easy, efficient manner. If you like what you see, feel free to subscribe and follow me for updates. If you have any questions, leave them below. I try to answer as many questions as possible.
Geometry Proofs Explained! Triangle Congruence
Triangle Congruence Theorems, Two Column Proofs, SSS, SAS, ASA, AAS Postulates, Geometry Problems
Triangle Congruence Proofs Practice with CPCTC!
Can You Prove the Triangle Inequality?
Proving triangle congruence | Congruence | High school geometry | Khan Academy
How to Do Triangle Geometry Proofs : Math Made Easy
Triangle Similarity - AA SSS SAS & AAA Postulates, Proving Similar Triangles, Two Column Proofs
Proving Triangle Congruence and Similarity
12 Class Math Exercise 6.3 Complete || 2nd Year Mathematics Exercise 6.3 Complete
How many ways are there to prove the Pythagorean theorem? - Betty Fei
Proof: Sum of measures of angles in a triangle are 180 | Geometry | Khan Academy
Proof of the Sum of Angles of a Triangle Measure 180 Degrees | Don't Memorise
Triangle Congruence Theorems Explained: ASA, AAS, HL
GCSE Maths - Congruent Triangle Rules #103
Triangle Congruence Proofs Explained SSS, SAS, ASA, AAS, HL
How to lie using visual proofs
Area of Triangle = ½ x b x h Why? | Fun Math | Don't Memorise
Triangle Inequality for Real Numbers Proof
CPCTC Geometry Proofs Made Easy, Triangle Congruence - SSS, SAS, ASA, & AAS, Two Colmn Proofs
Show that this triangle is Isosceles (OR equilateral OR scalene)
Using a Two Column Proof to Prove Two Sides of a Triangle are Equal
How to Determine Corresponding Parts of a Triangle - Congruent Triangles
Geometry: Sum of the angles in a triangle (a one-minute proof)
Equiangular Triangle Theorem
Комментарии
 0:09:43
0:09:43
 0:50:27
0:50:27
 0:09:06
0:09:06
 0:03:01
0:03:01
 0:04:18
0:04:18
 0:02:22
0:02:22
 0:29:23
0:29:23
 0:05:08
0:05:08
 0:22:05
0:22:05
 0:05:17
0:05:17
 0:04:28
0:04:28
 0:03:09
0:03:09
 0:07:25
0:07:25
 0:05:59
0:05:59
 0:15:25
0:15:25
 0:18:49
0:18:49
 0:01:01
0:01:01
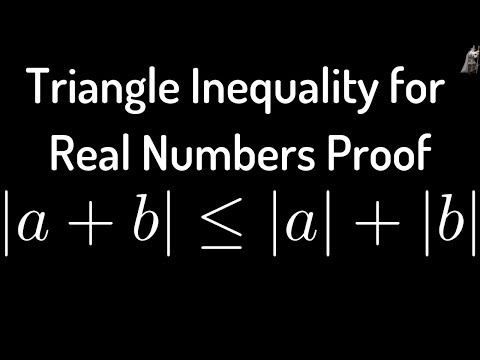 0:03:08
0:03:08
 0:52:00
0:52:00
 0:06:22
0:06:22
 0:05:24
0:05:24
 0:01:45
0:01:45
 0:01:05
0:01:05
 0:05:56
0:05:56