filmov
tv
Solving x^x=2 (exact answer)
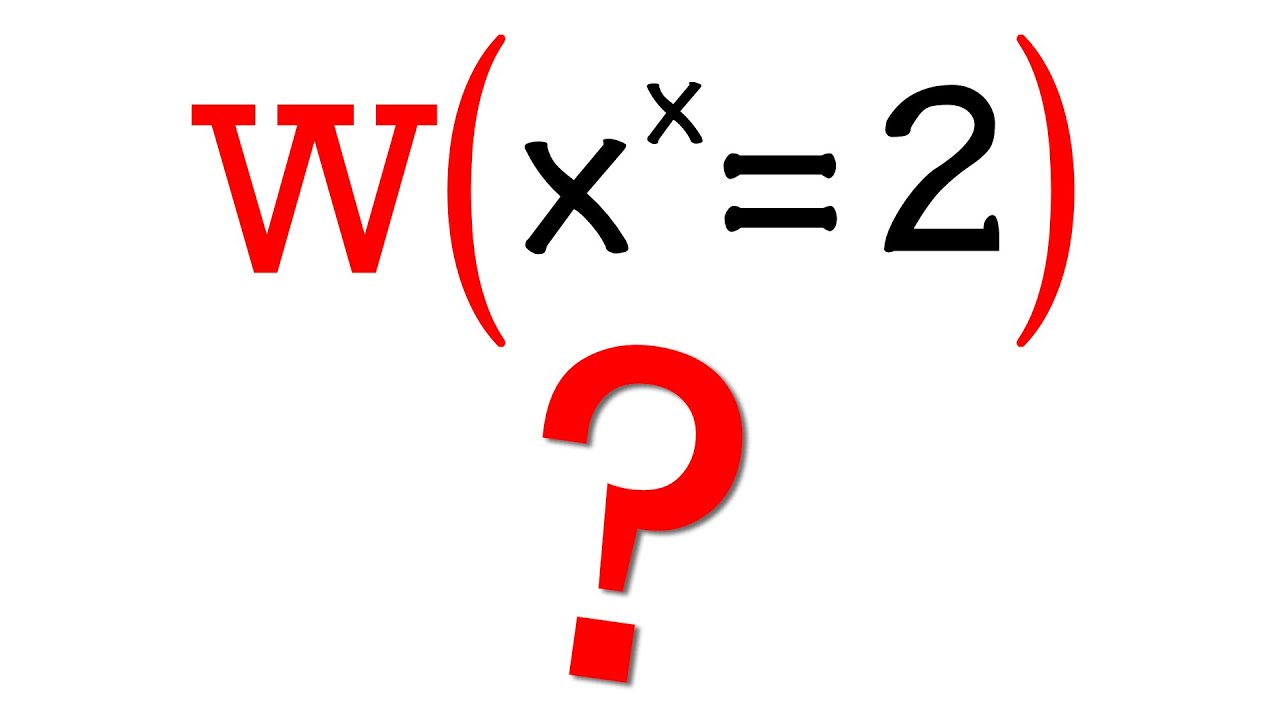
Показать описание
Solving x^x=2 (exact answer)
I couldn't solve x^x^x=2, so I solved x^x^(x+1)=2 instead
ALL solutions to x^2=2^x
Solving an Exact Differential Equation
Nice Olympiad Exponential Equation X^x=2^64 | Solve In 1 Minute
X^X =2^ 2048 | Solving a nice exponential equation| Math Olympiad Problem
Differentiation vol-2 EXACT EQUATION by Srinivasa rao
Solve an exponential equation by taking log of both sides & approximating the value
Trigonometry Question 5 - 7 Mathematics Paper 2 Grade 12 Pretrial 2023 Gauteng
Can you solve (x^x) - 2^(3x+192)=0 for X ?| Math Olympiad Training
solving the tetration equation x^x^x=2 by using Newton's Method
How do you solve an exponential equation with e as the base
Solve Exponential Equation Using Common Logarithms. Find Exact and Approx. Answers
Olympiad Math Question | Exponential Equation | Solve x^x = x^2
Solving x^sqrt(x)=1/2, an Exponential Equation
How to Solve 2^(x - 2) = 3^(2x - 4) Exponential Equation with Different Base with Logarithms
How to solve an exponential equation with two different bases
How to Solve Exponential Equations using Logarithms - No Common Base Present
2 different exponential equations
#quadratic #equation (2) #exact #answer
JEE Delight: Number of solutions of the equation x^2=e^x
Solving an natural logarithmic equation using properties of logs
Find the exact solution to the equation by completing the square x^2 -14x +19 = 0
Rearrange to find exact solution of 3∛(x^2 )=√6 Radical Equation
Комментарии
 0:10:07
0:10:07
 0:06:55
0:06:55
 0:13:21
0:13:21
 0:02:46
0:02:46
 0:01:37
0:01:37
 0:04:25
0:04:25
 0:03:59
0:03:59
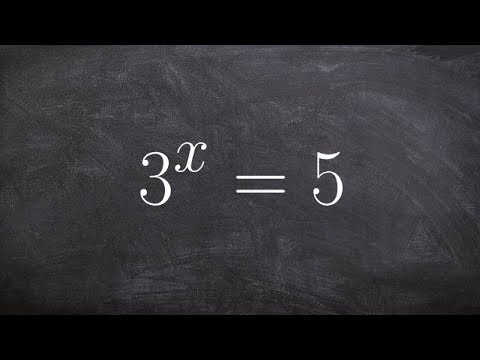 0:03:23
0:03:23
 1:29:10
1:29:10
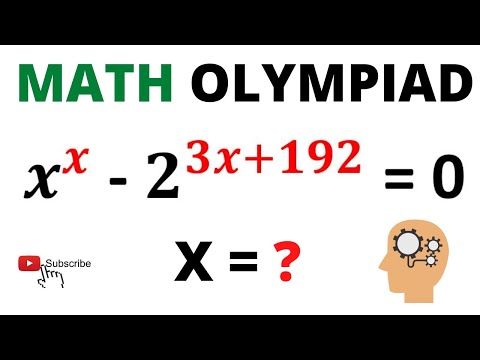 0:03:06
0:03:06
 0:07:02
0:07:02
 0:02:47
0:02:47
 0:06:00
0:06:00
 0:05:45
0:05:45
 0:09:57
0:09:57
 0:05:06
0:05:06
 0:05:11
0:05:11
 0:05:47
0:05:47
 0:09:19
0:09:19
 0:00:25
0:00:25
 0:01:28
0:01:28
 0:01:15
0:01:15
 0:03:56
0:03:56
 0:03:03
0:03:03