Solve Exponential Equation Using Common Logarithms. Find Exact and Approx. Answers

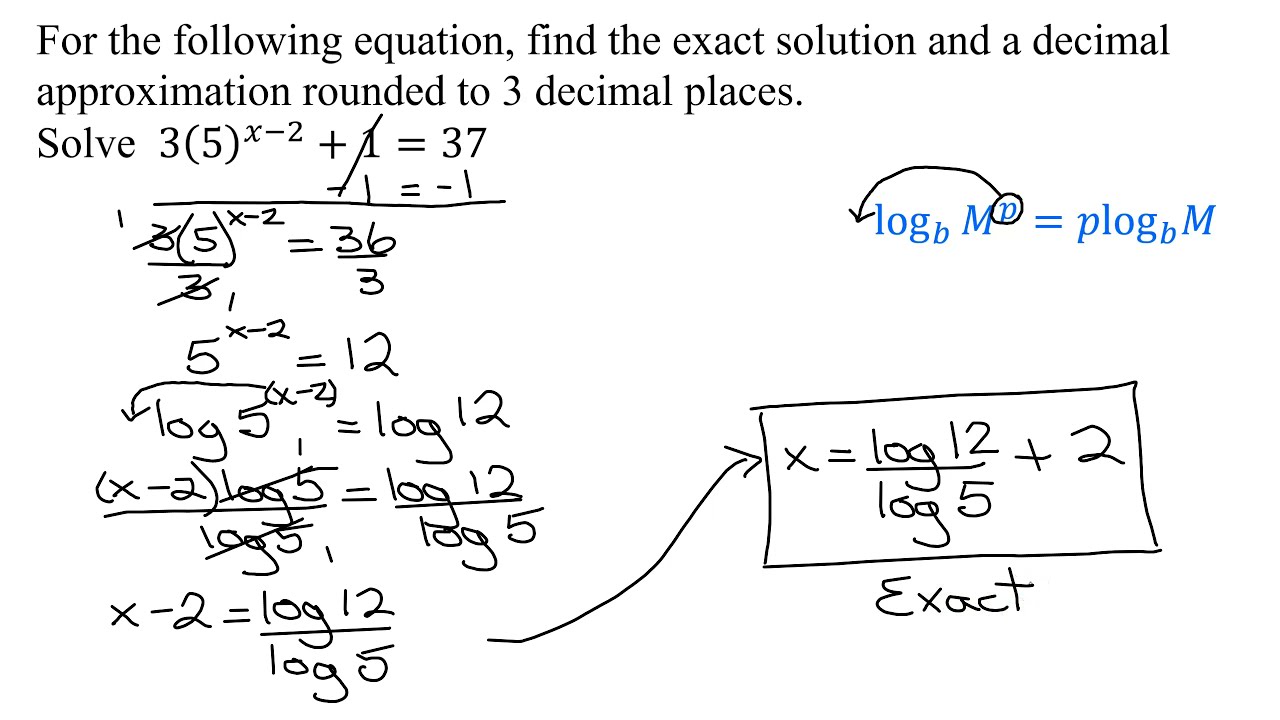
The exponential equation to be solved is 3(5)^(x-2)+1=37. As there is only one exponential expression, it has to be isolated on one side of the equation giving 5^(x-2)=12. As the bases can not be made the same, common logarithms are taken of both sides of the equation. The equation is then simplified using the power property of logarithms which results in a linear equation in x. The exact answer is found and then a calculator is used to find a decimal approximation (rounded to three decimal places).

Timestamps
0:00 Introduction
0:38 Isolate Exponential Expression
1:40 Take Common Logarithms of Both Sides of Equation
2:30 Use Power Property of Logarithms
3:40 Exact Solution
4:10 TI-84 Calculator
5:35Approximate Solution