filmov
tv
ALL solutions to x^2=2^x
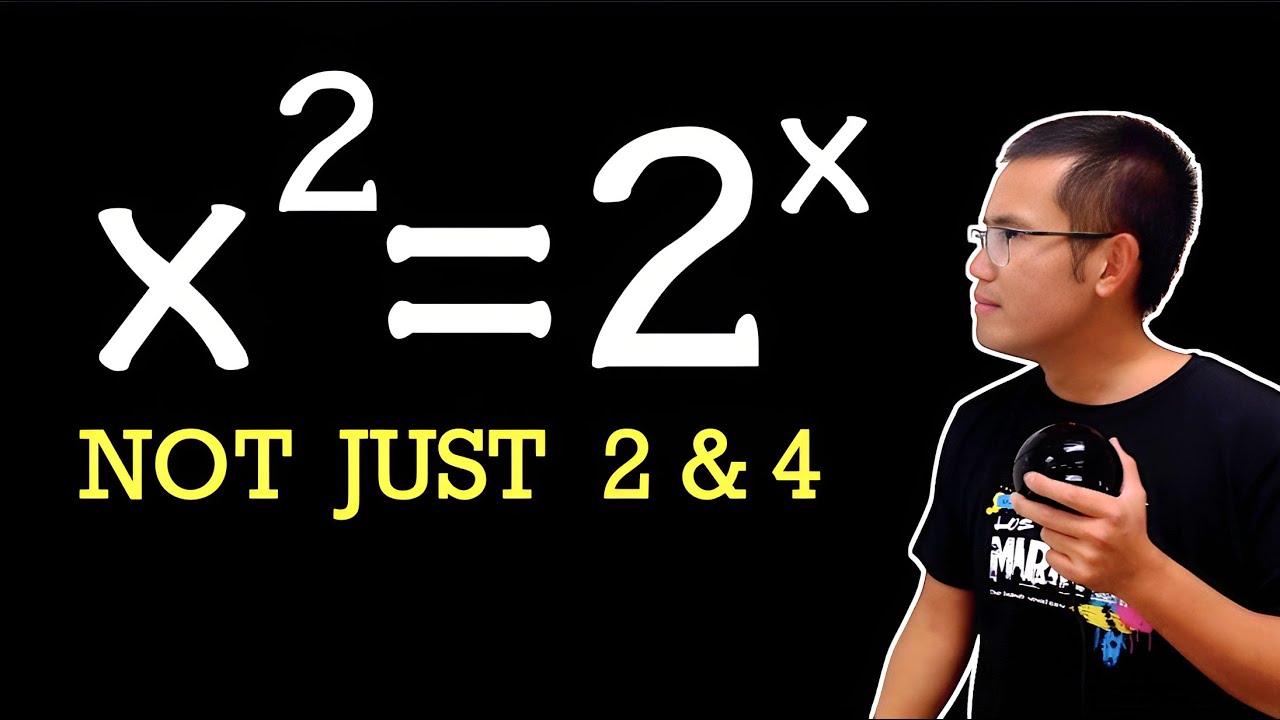
Показать описание
This is my "equation of the year" in 2019.
ALL solutions to x^2=2^x
A Nice Exponential Equation, x²=2ˣ
What is the product of all the solutions of (x + 2)^2 = |x + 2|?
The famous exponential equation 2^x=2x (ALL solutions)
5 simple unsolvable equations
Common Math Error: Find All Solutions to x^2=2x #maths #math
Solving using the quadratic formula with complex solutions
Solving an equation with variables on both side and one solution
Quadratic Equations | Solve by factoring | Free Math Videos
The product of all the solutions of the equation`(x-2)^(2)-3|x-2|+2=0` is
Solving x^2+9=0
How To Solve Absolute Value Equations, Basic Introduction, Algebra
Solve quadratic equation by factorisation
Solving x^x=2 (exact answer)
How To Solve Quadratic Equations Using The Quadratic Formula
How to Solve x^2 - x + 2 = 0 by Factoring
How to solve a polynomial inequality?
Rubik’s Cube solved with 2 Moves???? 😅
Algebra - How To Solve Equations Quickly!
How REAL Men Integrate Functions
Expanding Brackets
When mathematicians get bored (ep1)
How to Solve x^2 + 2x + 1 = 0 by Factoring
The set of all solutions of the inequation `x^2-2x+5 lt=0` is
Комментарии
 0:13:21
0:13:21
 0:10:34
0:10:34
 0:01:53
0:01:53
 0:10:28
0:10:28
 0:00:50
0:00:50
 0:00:47
0:00:47
 0:05:28
0:05:28
 0:02:36
0:02:36
 0:02:43
0:02:43
 0:02:36
0:02:36
 0:03:44
0:03:44
 0:04:21
0:04:21
 0:09:05
0:09:05
 0:10:07
0:10:07
 0:05:56
0:05:56
 0:01:59
0:01:59
 0:00:58
0:00:58
 0:00:17
0:00:17
 0:25:05
0:25:05
 0:00:35
0:00:35
 0:00:51
0:00:51
 0:00:37
0:00:37
 0:02:15
0:02:15
 0:02:53
0:02:53