filmov
tv
solving the tetration equation x^x^x=2 by using Newton's Method
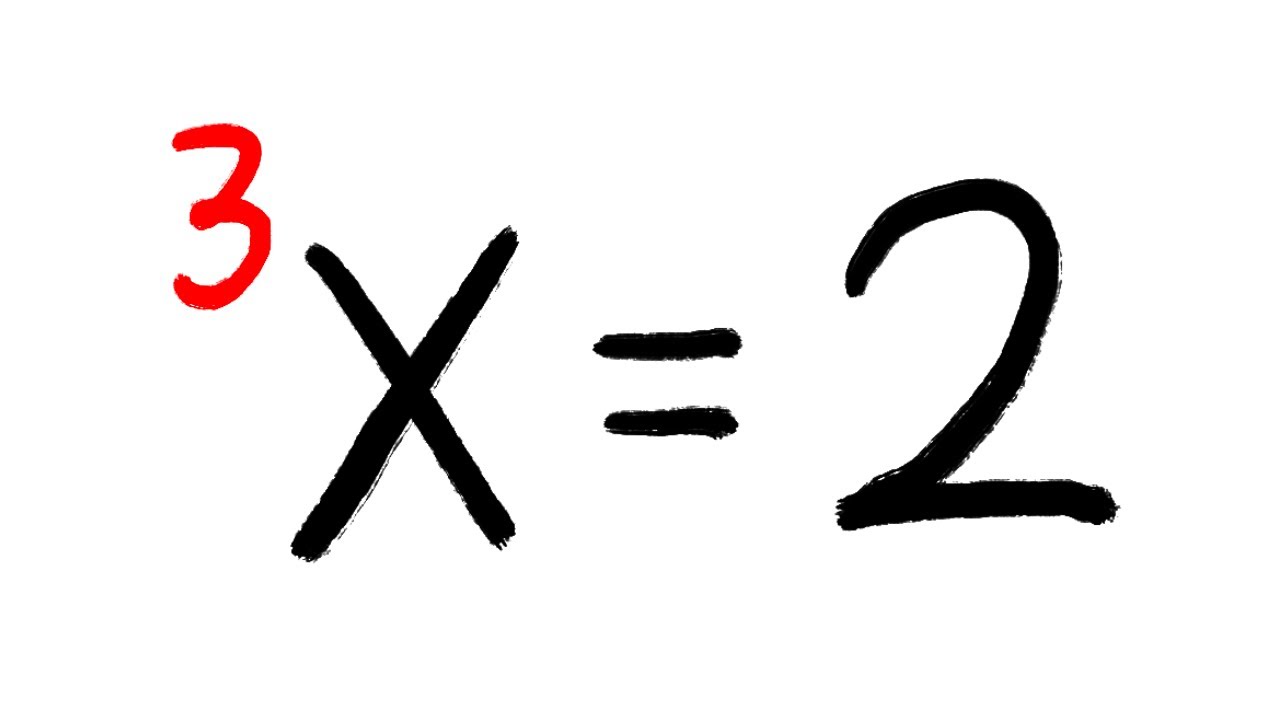
Показать описание
Here's an interesting tetration equation x^x^x=2 that looks solvable with the Lambert W function but is not.
#calculus #blackpenredpen #math
#calculus #blackpenredpen #math
solving the tetration equation x^x^x=2 by using Newton's Method
Solving a tetration equation
Infinite tetration of rad2 = 2 [tetration]
Tetration equation
Why you didn't learn tetration in school[Tetration]
Solving x^x=2 (Lambert W function)
Can You Solve x^x^x^... = 2? Infinite Exponent Tower Trick
The Tetration Equation: Solve (x^2)(x^x) = x^(x^x)
Lambert W Function
Why use tetration? #shorts
Cracking the Tetration Code: Solving ²x = 2ˣ
Beyond Exponentiation: A Tetration Investigation
Derivatives of x^x and x^x^x (2nd and 3rd tetrations of x)
x↑↑2 = 16
Basic tetration introduction
5 simple unsolvable equations
The Tetration Equation Challenge: Are You Ready?
Solving Tetration Equation One Step at a Time
Solving the Tetration Equation ^32^x + 4^x = 6 Step by Step Explanation
The Hardest Math Test
I couldn't solve x^x^x=2, so I solved x^x^(x+1)=2 instead
Solve for x | Exponential Equations | Mathematics
'Prove' 4 = 2. Can You Spot The Mistake?
Defining the natural logarithm
Комментарии
 0:07:02
0:07:02
 0:07:17
0:07:17
 0:12:34
0:12:34
 0:10:26
0:10:26
 0:06:23
0:06:23
 0:10:07
0:10:07
 0:01:00
0:01:00
 0:09:13
0:09:13
 0:14:35
0:14:35
 0:00:40
0:00:40
 0:03:59
0:03:59
 0:24:46
0:24:46
 0:09:11
0:09:11
 0:08:21
0:08:21
 0:05:06
0:05:06
 0:00:50
0:00:50
 0:09:32
0:09:32
 0:08:16
0:08:16
 0:12:13
0:12:13
 0:00:28
0:00:28
 0:06:55
0:06:55
 0:04:29
0:04:29
 0:06:37
0:06:37
 0:00:56
0:00:56