filmov
tv
Olympiad Math Question | Exponential Equation | Solve x^x = x^2

Показать описание
Olympiad Math Question are one of the tough, complex and sometimes confusing mathematics to solve.
But this can be disputed when you know the rules of mathematics.
In this video I will show you how to solve exponential of this kind quick with easy through the application of some mathematical laws.
Here, you will learn how to make use of the division law of indices and the power law of logarithm.
I will show you how to introduce or use natural logarithm in solving this kind of exponential equation in order to get the true value(s) of the variable in question.
I will also introduce you to the zero product property use in solving quadratic equations by factorization.
These and many more ideas to learn from this video and to get all of them, kindly stay till the end from the beginning of this video without skipping any part.
Also subscribe to this channel in order to get more and better knowledge in mathematics.
Happy watching
But this can be disputed when you know the rules of mathematics.
In this video I will show you how to solve exponential of this kind quick with easy through the application of some mathematical laws.
Here, you will learn how to make use of the division law of indices and the power law of logarithm.
I will show you how to introduce or use natural logarithm in solving this kind of exponential equation in order to get the true value(s) of the variable in question.
I will also introduce you to the zero product property use in solving quadratic equations by factorization.
These and many more ideas to learn from this video and to get all of them, kindly stay till the end from the beginning of this video without skipping any part.
Also subscribe to this channel in order to get more and better knowledge in mathematics.
Happy watching
A Nice Math Olympiad Exponential Equation 3^x = X^9
Germany - Math Olympiad Exponential Problem.
United States l can you solve?? l Olympiad Math Exponential Fractional problem l x?
Olympiad Mathematics Question | Exponential Equation
A Nice Olympiad Exponential Multiplication Problem #short #olympiad #mathematics #maths #exponents
Japanese l can you solve?? l Olympiad Math Exponential Problem l find m?
Mexico - A Nice Math Olympiad Exponential Problem
Olympiad Mathematics Question || Solving Olympiad Exponential Equation
A awesome mathematics exponential problem | Olympiad Question | x=?
Italy l Very Nice Olympiad Math Exponential Problem l find value of x?
Exponents problem | Math Olympiad questions
Olympiad Mathematics | Learn how to solve exponential equation quickly | Math Olympiad Training
Math Olympiad Question | Equation solving | You should learn this trick to pass the exam
United Kingdom - A Nice Exponential Equation | Math olympiad Question
Solve exponents problem | Math Olympiad question
A Nice Math Problem With Exponents| Math Olympiad
A awesome mathematics exponential problem | Olympiad Question | x=?
A Nice Exponential Equation • x=? #shorts #olympiad #mathematics #maths #matholympiad #exponents
Olympiad Mathematics | Two Methods to Solve System of Exponential Equations | Math Olympiad Training
A Nice Olympiad Exponential Equation | Exponential Equation | Olympiad Math Question.
Math Olympiad| German| exponential math problem.
Korean Math Olympiad Question | A Nice Exponential Problem
A nice Exponential Problem | Olympiad Math Problem Solving | Exponent ke Sawal
A Nice Algebra Math Problem On Expansion. #shorts #math #olympiad #mathematics #matholympiad #viral
Комментарии
 0:02:34
0:02:34
 0:04:45
0:04:45
 0:14:52
0:14:52
 0:05:41
0:05:41
 0:00:52
0:00:52
 0:10:47
0:10:47
 0:08:36
0:08:36
 0:14:46
0:14:46
 0:12:22
0:12:22
 0:17:10
0:17:10
 0:01:17
0:01:17
 0:08:04
0:08:04
 0:01:54
0:01:54
 0:09:19
0:09:19
 0:01:50
0:01:50
 0:03:12
0:03:12
 0:12:17
0:12:17
 0:01:00
0:01:00
 0:10:06
0:10:06
 0:19:27
0:19:27
 0:07:31
0:07:31
 0:03:15
0:03:15
 0:04:48
0:04:48
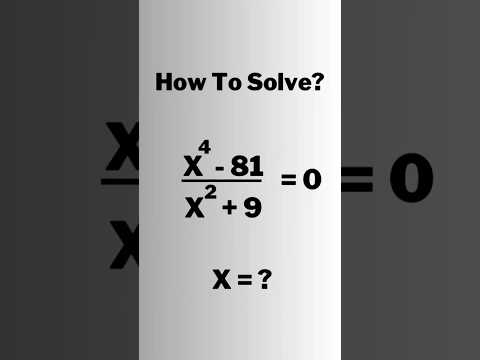 0:00:55
0:00:55