filmov
tv
A Factorial Equation | Math Olympiads

Показать описание
🤩 Hello everyone, I'm very excited to bring you a new channel (SyberMath Shorts)
Enjoy...and thank you for your support!!! 🧡🥰🎉🥳🧡
If you need to post a picture of your solution or idea:
#NumberTheoryProblems #FactorialEquations #Factorials
via @YouTube @Apple @Desmos @NotabilityApp @googledocs @canva
PLAYLISTS 🎵 :
Enjoy...and thank you for your support!!! 🧡🥰🎉🥳🧡
If you need to post a picture of your solution or idea:
#NumberTheoryProblems #FactorialEquations #Factorials
via @YouTube @Apple @Desmos @NotabilityApp @googledocs @canva
PLAYLISTS 🎵 :
A Factorial Equation | Math Olympiads
A Factorial Equation | Math Olympiads
A nice factorial equation: The math behind solving equations.
Factorials Explained!
A Factorial Equation | n! = 6!7!
a nice factorial equation.
A Factorial equation: Simple but tricky #Shorts
A Factorial Equation With Integers
Project152 Week 30 Solutions
Solving the hardest question of a British Mathematical Olympiad
USA | A nice factorial equation | math Olympiad problem
A very interesting factorial based sum
Solving A Factorial Equation | How To Solve Factorial Equation Without Using Mathematical Induction?
15! / 17! - 16! Many failed!! #maths #mathematics #factorial
Factorial Equation
Factorial (!) ? | Fun Math | Don't Memorise
How to Take the Factorial of Any Number
Brazil | A nice factorial equation | math Olympiad
A Nice Math Factorial Problem • Evaluate #shorts #olympiad #mathematics #maths #matholympiad #tips
Math Olympiad Preparation | A Nice Factorial Problem | Calculate Without Calculators...
Factorial Equation
A Factorial Equation #maths #matholympiad #education #factorials #factorial
A Factorial Equation | n! = n^2 + 19n
How to Find the Limit of a Factorial Function : Principles of Math
Комментарии
 0:09:46
0:09:46
 0:00:48
0:00:48
 0:10:54
0:10:54
 0:11:17
0:11:17
 0:08:25
0:08:25
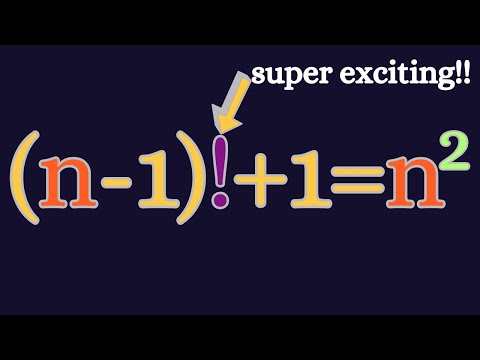 0:10:16
0:10:16
 0:00:40
0:00:40
 0:08:49
0:08:49
 0:41:59
0:41:59
 0:11:26
0:11:26
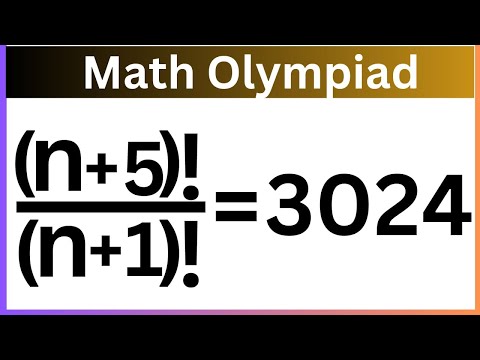 0:11:10
0:11:10
 0:08:31
0:08:31
 0:05:09
0:05:09
 0:01:51
0:01:51
 0:00:49
0:00:49
 0:00:45
0:00:45
 0:26:31
0:26:31
 0:08:56
0:08:56
 0:00:40
0:00:40
 0:06:19
0:06:19
 0:00:46
0:00:46
 0:00:47
0:00:47
 0:00:44
0:00:44
 0:02:00
0:02:00