filmov
tv
Brazil | A nice factorial equation | math Olympiad
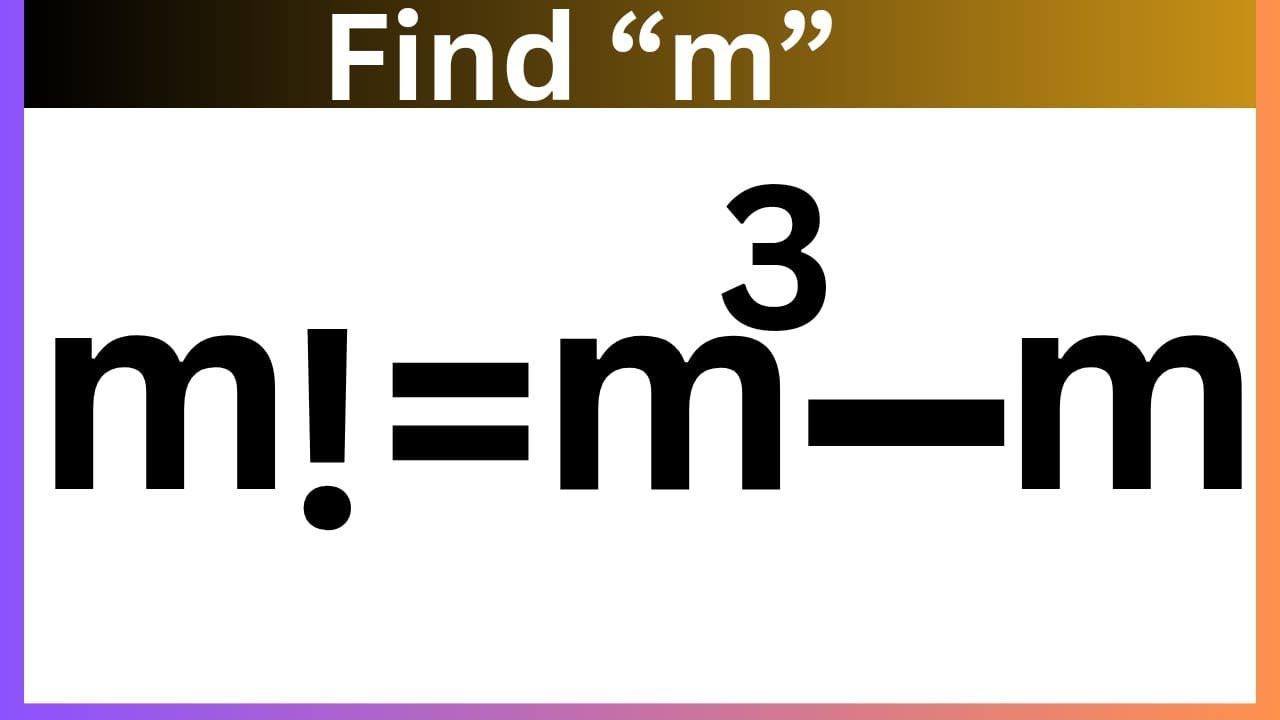
Показать описание
Hello viewers
This is your love for me
If you like my YouTube video Brazil | A nice factorial equation | math Olympiad please like share and subscribe my YouTube channel. If you have any question related to maths feel easy to ask me I will upload a video for you
#Mrmath11#lklogic#integral#maths#olympiadmathquestion#algebra#exponentialequation#exponents#vedicmaths#integral#how#lesson#mathsclass#viral#lklogic#viralmathproblem#howtosolvemathspuzzles#howtosolveolympiadmathproblem#mathematics#mathematicslesson#matholympiad#internatinalmathoympiad#matholympiadequation#premath#sybermath#mathwindow#greqants#mathstudent#mathtrick#mathshorts#mathrubhuminews#ssc#ssccgl#upsc#upscaspirants#upscpreparation#mdcat#engineermuhammadalimirza#upscnotes#ecat#sindhtextbookboard
This is your love for me
If you like my YouTube video Brazil | A nice factorial equation | math Olympiad please like share and subscribe my YouTube channel. If you have any question related to maths feel easy to ask me I will upload a video for you
#Mrmath11#lklogic#integral#maths#olympiadmathquestion#algebra#exponentialequation#exponents#vedicmaths#integral#how#lesson#mathsclass#viral#lklogic#viralmathproblem#howtosolvemathspuzzles#howtosolveolympiadmathproblem#mathematics#mathematicslesson#matholympiad#internatinalmathoympiad#matholympiadequation#premath#sybermath#mathwindow#greqants#mathstudent#mathtrick#mathshorts#mathrubhuminews#ssc#ssccgl#upsc#upscaspirants#upscpreparation#mdcat#engineermuhammadalimirza#upscnotes#ecat#sindhtextbookboard
Brazil | A nice factorial equation | math Olympiad 🤔
Brazil | A nice factorial equation | math Olympiad
Brazil | A nice factorial equation | Math Olympiad
Brazil | A nice Factorial Equation | Logarithmic Problem | Exponent Simplification | Math Olympiad
Brazil math olympiad factorial problem | A nice factorial question |
Brazil math olympiad factorial problem | A nice factorial question |
Brazil | can you solve | a nice factorial equation | math Olympiad
Brazil | you should know | a nice factorial equation
Brazil | A nice factorial equation to solve| Olympiad question #math #matholympiad
Brazil | A nice factorial equation | Math Olympiad
Brazil math olympiad problem | A nice factorial problem |
Brazil | A Nice Factorial Equation | Math Olympiad | Find the value of m
8^logx-2^logx=5! | Brazil | A Nice Factorial Problem
A Nice Factorial problem | Interesting Solution !!!
Emporium mall me Is larki ki bygarti deko
A nice factorial problem |Solve for n#math #factorial #matholympiad
A Nice Olympiad Factorial Problem || How to Simplify Factorials: √(12!) / √(5!) Explained!
A Nice Math Factorial Expression #shorts #olympiad #maths #matholympiad #mathematics #factorial
Factorial Simplification #themathscholar23 #mathematics #math #factorial #factorialnotation #satmath
A nice Math Olympiad Algebra | Factorial Simplification | #mathematics #algebra #factorial
Factorial Math Simplification #factorialnotation #factorials #divisiontricks #themathscholar23 #sat
A nice Algebra Problem | Math Olympiad | Quadratic Factorial Question | Can you solve this ? #maths
A Nice Factorial Math Olympiad Problem | Find the value of n ?
A Nice factorial Problem 🤔 | Maths Olympiad #factorial problem #matholympaid#maths
Комментарии
 0:07:02
0:07:02
 0:08:56
0:08:56
 0:05:53
0:05:53
 0:13:26
0:13:26
 0:03:54
0:03:54
 0:02:42
0:02:42
 0:09:35
0:09:35
 0:05:18
0:05:18
 0:11:23
0:11:23
 0:10:09
0:10:09
 0:02:53
0:02:53
 0:10:28
0:10:28
 0:06:10
0:06:10
 0:04:39
0:04:39
 0:00:18
0:00:18
 0:10:38
0:10:38
 0:02:31
0:02:31
 0:00:44
0:00:44
 0:00:11
0:00:11
 0:08:37
0:08:37
 0:00:13
0:00:13
 0:11:07
0:11:07
 0:02:39
0:02:39
 0:07:40
0:07:40