filmov
tv
a nice factorial equation.

Показать описание
If you are going to use an ad-blocker, considering using brave and tipping me BAT!
Books I like:
Abstract Algebra:
Differential Forms:
Number Theory:
Analysis:
Calculus:
My Filming Equipment:
A Nice Factorial Equation
A nice factorial equation: The math behind solving equations.
a nice factorial problem
a nice factorial equation.
Can We Solve A Nice Factorial Equation
Math Olympiad Preparation | A Nice Factorial Problem | Calculate Without Calculators...
A Nice Math Factorial Problem • Evaluate #shorts #olympiad #mathematics #maths #matholympiad #tips
Let's Solve A Nice Factorial Equation
what is the value of X ? | A nice factorial equation to solve
A Nice Factorial Equation 🔥• X= ?
Factorial Equation
Brazil | A nice factorial equation | math Olympiad
Math Olympiad | A Nice Algebra Problem | A Nice Factorial Equation
Norway - Math Olympiad Question | A Nice Factorial Problem
USA | A nice factorial equation | math Olympiad problem
A Beautiful Exponential Problem Olympiad Math || A Nice Factorial Equation
A mysterious factorial equation.
A Nice Factorial Equation | n!=2^n
Factorials Explained!
How to Take the Factorial of Any Number
A Nice And Perfect Factorial Equation
Math Olympiad Question, A Nice Factorial Math Problems 𝟕!×𝟐!=𝒎!, Math Olympiad Challenge
A nice math problem about factorial
A Nice Factorial Equation | x!=6!7!
Комментарии
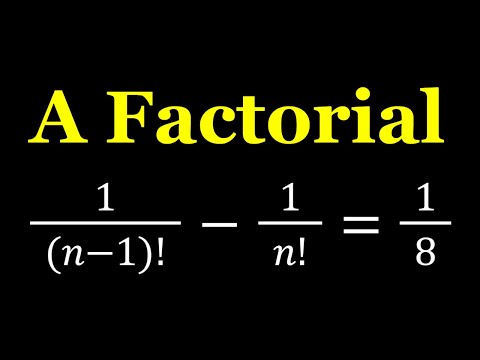 0:08:38
0:08:38
 0:10:54
0:10:54
 0:00:37
0:00:37
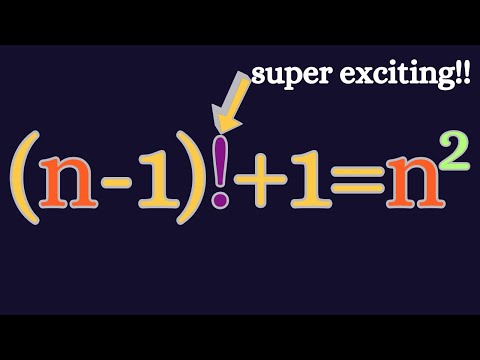 0:10:16
0:10:16
 0:09:31
0:09:31
 0:06:19
0:06:19
 0:00:40
0:00:40
 0:10:28
0:10:28
 0:03:37
0:03:37
 0:02:09
0:02:09
 0:00:49
0:00:49
 0:08:56
0:08:56
 0:08:07
0:08:07
 0:02:35
0:02:35
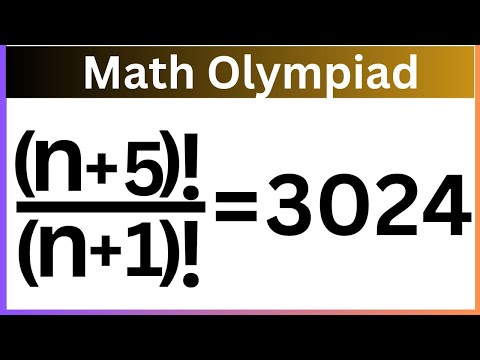 0:11:10
0:11:10
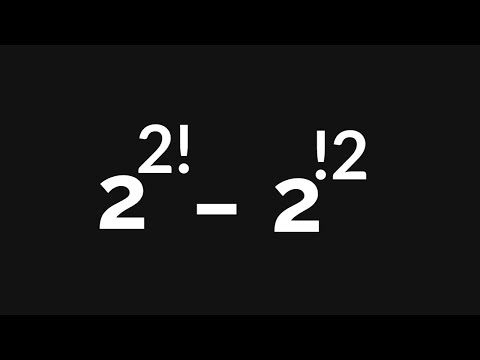 0:02:57
0:02:57
 0:14:28
0:14:28
 0:09:32
0:09:32
 0:11:17
0:11:17
 0:26:31
0:26:31
 0:05:26
0:05:26
 0:03:30
0:03:30
 0:02:04
0:02:04
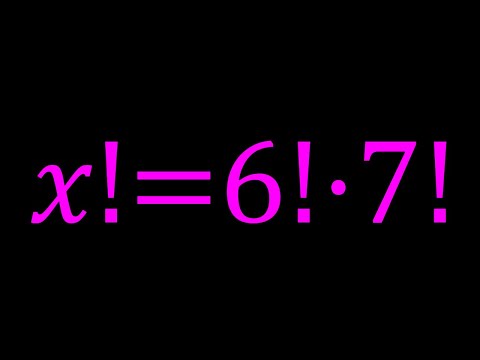 0:08:33
0:08:33