filmov
tv
Solving A Factorial Equation | How To Solve Factorial Equation Without Using Mathematical Induction?
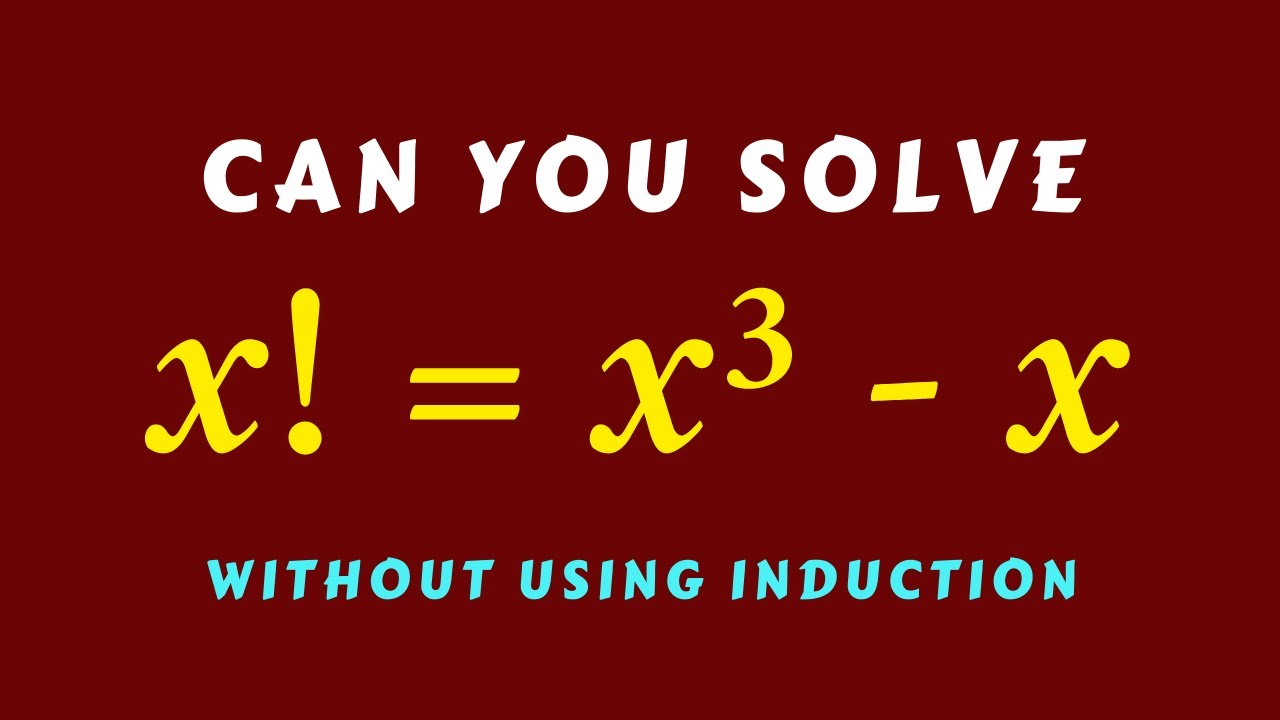
Показать описание
How to solve a factorial equation x! = x³ - x
Solve Equation with Factorials
how to solve a factorial equation?
Can You Solve this Factorial Equation? | Fast & Easy Tutorial
Factorials Explained!
How to solve equations with Factorials
How to solve factorial equations
Solving Factorial Expressions in One Minute (2024) | Solve factorial equation
A Nice Factorial Equation
Mathematics P1 Nov 2005/ Grade 12 Final revision ( tricks and techniques)!@ zamokuhlemakhamba
Solve factorial equation
How to solve factorial equations?
A nice factorial equation: The math behind solving equations.
Nice Factorial Equation - Can You Solve It?
Solving A Cool Factorial Equation: Math behind Solution
Can you solve it? | Factorial equation
Let's Solve A Nice Factorial Equation | Harvard-MIT
Can you solve it? | How to solve? | Factorial Equation
Factorial Algebra Solve Equation Combinatorics
Solving Factorial Equation
Solving Factorial Equation
Can You Solve This Factorial Equation | Solve for n | Number Theory
Solving Factorial Equations: Find the Value of X | Olympiad Exam Preparation
How to Take the Factorial of Any Number
A Factorial Equation | Can you solve?
Комментарии
 0:03:25
0:03:25
 0:02:22
0:02:22
 0:04:45
0:04:45
 0:11:17
0:11:17
 0:03:01
0:03:01
 0:03:34
0:03:34
 0:01:46
0:01:46
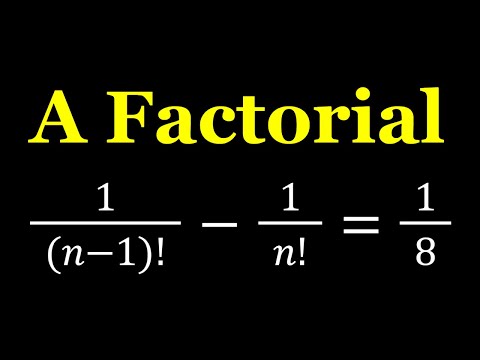 0:08:38
0:08:38
 6:17:03
6:17:03
 0:06:31
0:06:31
 0:03:03
0:03:03
 0:10:54
0:10:54
 0:04:43
0:04:43
 0:10:52
0:10:52
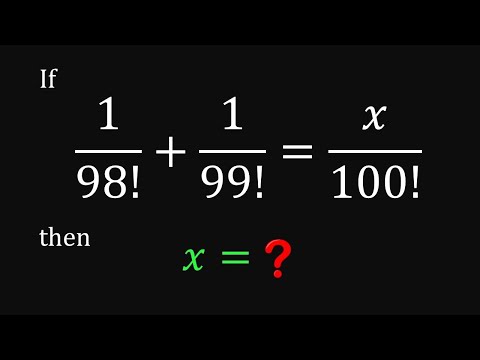 0:03:39
0:03:39
 0:10:56
0:10:56
 0:02:51
0:02:51
 0:04:26
0:04:26
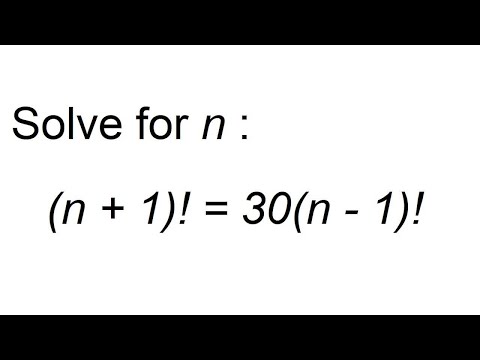 0:04:20
0:04:20
 0:02:44
0:02:44
 0:04:43
0:04:43
 0:11:27
0:11:27
 0:26:31
0:26:31
 0:08:20
0:08:20