filmov
tv
Comparing 5^23 and 7^15
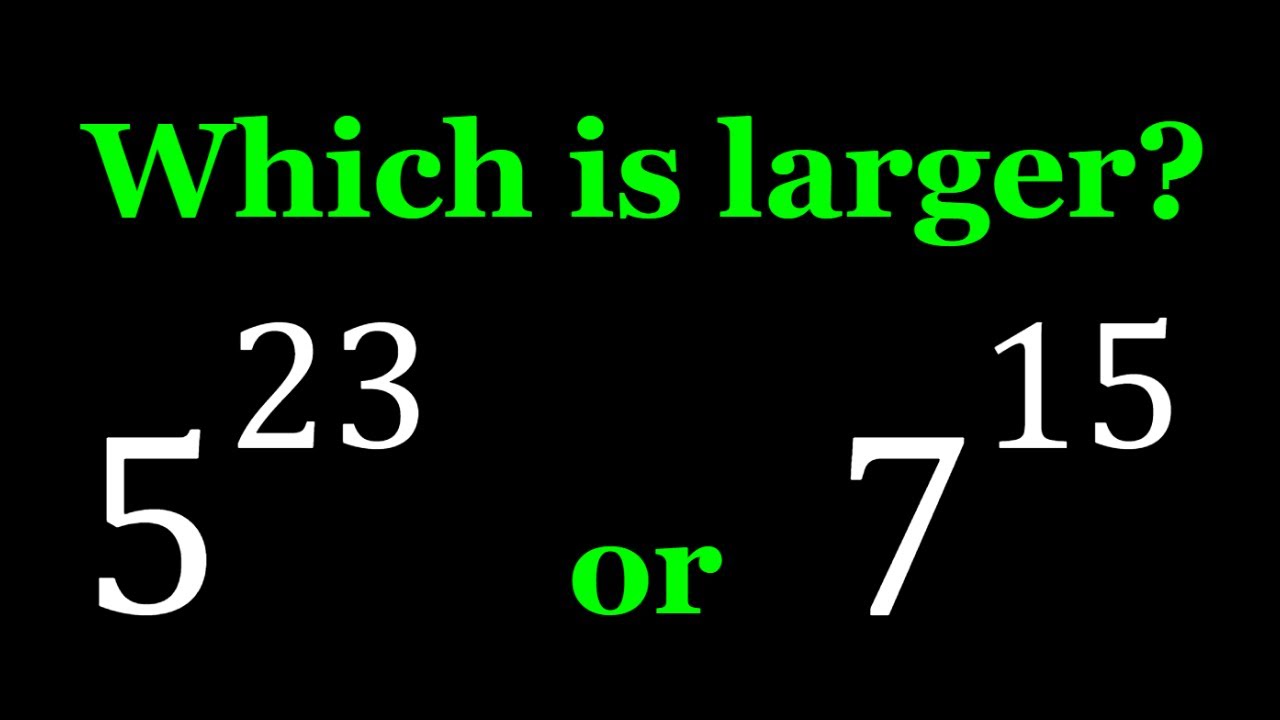
Показать описание
If you need to post a picture of your solution or idea:
#ChallengingMathProblems #ComparingNumbers
PLAYLISTS 🎵 :
#ChallengingMathProblems #ComparingNumbers
PLAYLISTS 🎵 :
How to Compare 5^23 and 7^15
Comparing 5^23 and 7^15
Samsung S23 VS iPhone 15 - Battery Drain Test Comparison
Galaxy S23 vs iPhone 14 vs Pixel 7! Camera Comparison Test! | VERSUS
iPhone 15 vs Google Pixel 7 battery comparison!
Summer 2023 WR Comparison - Day 1 vs Day 7 vs Day 90
Summer 2024 WR Comparison - Day 1 vs Day 7 vs Day 90
Garten of Banban 1,2,3,4,6,7 HEIGHT COMPARISON + THEIR VOICE Size Comparison of Garten of Banban
Which Rubik’s Clock Method Is The Best? Full Method Comparison
Google pixel 7 vs Google pixel 7 Pro compare with iPhone 15 pro and max #tech #smartphone #shorts
Comparing 3:4 to 5:7 Polyrhythm
iPhone 15 Pro vs S23 Ultra vs Pixel 7 Camera Comparison
iPhone 16 Pro Max vs 15 Pro Max / Pixel 9 Pro XL / Samsung / Huawei / Xiaomi Battery Life DRAIN Test
iPhone 16 Pro vs iPhone 16 Plus - Which To Choose?
iPhone 6 plus Vs iPhone 7 plus #iphone6plus #iphone7plus #comparison #shorts #viral #apple #appleiph
iPhone 16 vs. 16 Plus vs. 16 Pro vs. 16 Pro Max Battery Test!
Comparing Asus ROG Phone 7 vs iPhone 14 Pro Max: Ultimate comparison #shorts
Trailer Comparison: Garten Of Banban 1,2,3,4,6,7,8,9,10,11,12,13,14,15,16 | Garten Of Banban 7
Intel Core 7 150U vs Intel Core Ultra 5 238V Comparison
iPhone 15 vs Pixel 7 Pro Comparison #shorts
Trailer Comparison: Garten Of Banban 5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20 | Garten Of Banban 7
Intel Core 7 150U vs Intel Core Ultra 5 236V Comparison
Behind The Scenes History of Size Comparison Mar 15, 2022 7:15;00 PM - Apr 23, 2022 19:45;00 PM
Trailer Comparison: Garten Of Banban 1,2,3,4,5,6,7,8,9,10,11,12 | Evolution Of Garten Of Banban
Комментарии
 0:05:01
0:05:01
 0:05:01
0:05:01
 0:10:22
0:10:22
 0:15:01
0:15:01
 0:00:46
0:00:46
 0:14:36
0:14:36
 0:16:27
0:16:27
 0:08:11
0:08:11
 0:43:58
0:43:58
 0:00:07
0:00:07
 0:00:23
0:00:23
 0:05:50
0:05:50
 0:18:41
0:18:41
 0:16:17
0:16:17
 0:00:09
0:00:09
 0:07:15
0:07:15
 0:00:06
0:00:06
 0:12:36
0:12:36
 0:02:13
0:02:13
 0:00:11
0:00:11
 0:08:13
0:08:13
 0:02:13
0:02:13
 0:00:16
0:00:16
 0:11:25
0:11:25