filmov
tv
Evaluating a Logarithmic Expression in Three Ways
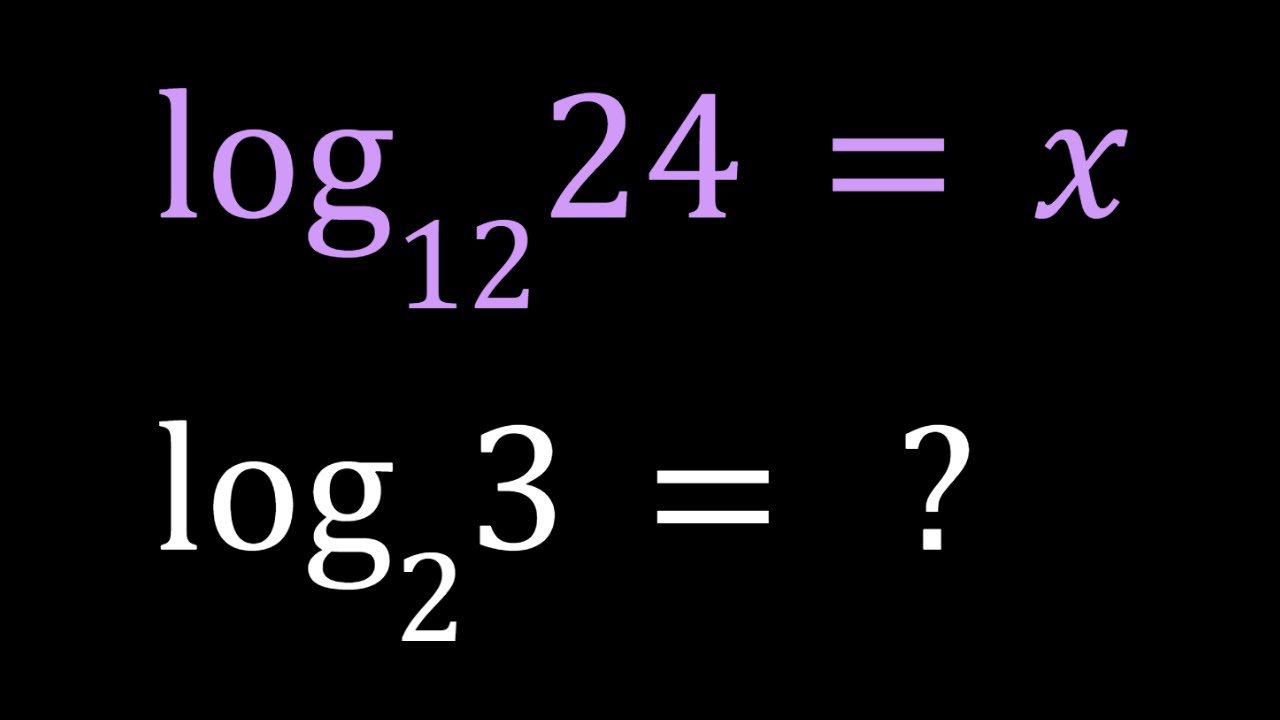
Показать описание
If you need to post a picture of your solution or idea:
#ChallengingMathProblems #LogarithmicExpressions
PLAYLISTS 🎵 :
#ChallengingMathProblems #LogarithmicExpressions
PLAYLISTS 🎵 :
Logarithms - The Easy Way!
Fancier logarithm expressions | Logarithms | Algebra II | Khan Academy
Evaluating logarithmic expressions
Evaluating a Logarithmic Expression in Three Ways
Evaluating Basic Logarithms Without a Calculator
Evaluating logarithmic expressions
ALEKS: Evaluating a logarithmic expression
Evaluating A Logarithmic Expression
AP Precalculus - Intro to Logarithms - Passwater 2.9
Pre-Calculus - Evaluating Logarithmic Expressions Using the Properties of Logarithms
How to Apply Logarithmic Laws and Evaluate Log Expressions
Evaluating A Logarithmic Expression
Master Evaluating a Logarithmic Expression using the Properties of Logarithms
Properties of Logarithms
Solving Logarithmic Equations
Pre-Calculus - Learn How To Evaluate a Logarithmic Expression
Ex 1: Evaluate a Logarithmic Expression Using the Properties of Logarithms
Pre-Calculus - Evaluating a Logarithm Without a Calculator
Evaluate this Logarithmic Expression in 1 Minute | Fast & Easy Explanation | No Calculators
The cleanest way of evaluating a logarithm
Algebra 2 - How to Evaluate a Logarithmic Expression Using Rules of Logarithms
Evaluate a Logarithmic Expression given Facts about a log (Properties of the Log)
Evaluating a Logarithmic Expression from Another One
Master Evaluating a Logarithmic Expressions using the one to one property
Комментарии
 0:10:20
0:10:20
 0:04:20
0:04:20
 0:01:53
0:01:53
 0:09:31
0:09:31
 0:03:27
0:03:27
 0:02:42
0:02:42
 0:00:32
0:00:32
 0:07:47
0:07:47
 0:16:29
0:16:29
 0:01:41
0:01:41
 0:06:12
0:06:12
 0:09:36
0:09:36
 0:07:29
0:07:29
 0:05:40
0:05:40
 0:25:27
0:25:27
 0:01:04
0:01:04
 0:04:43
0:04:43
 0:01:13
0:01:13
 0:04:24
0:04:24
 0:00:15
0:00:15
 0:01:15
0:01:15
 0:01:53
0:01:53
 0:05:12
0:05:12
 0:14:46
0:14:46