filmov
tv
Solving 7x^5+x+8 without Using the Quintic Formula
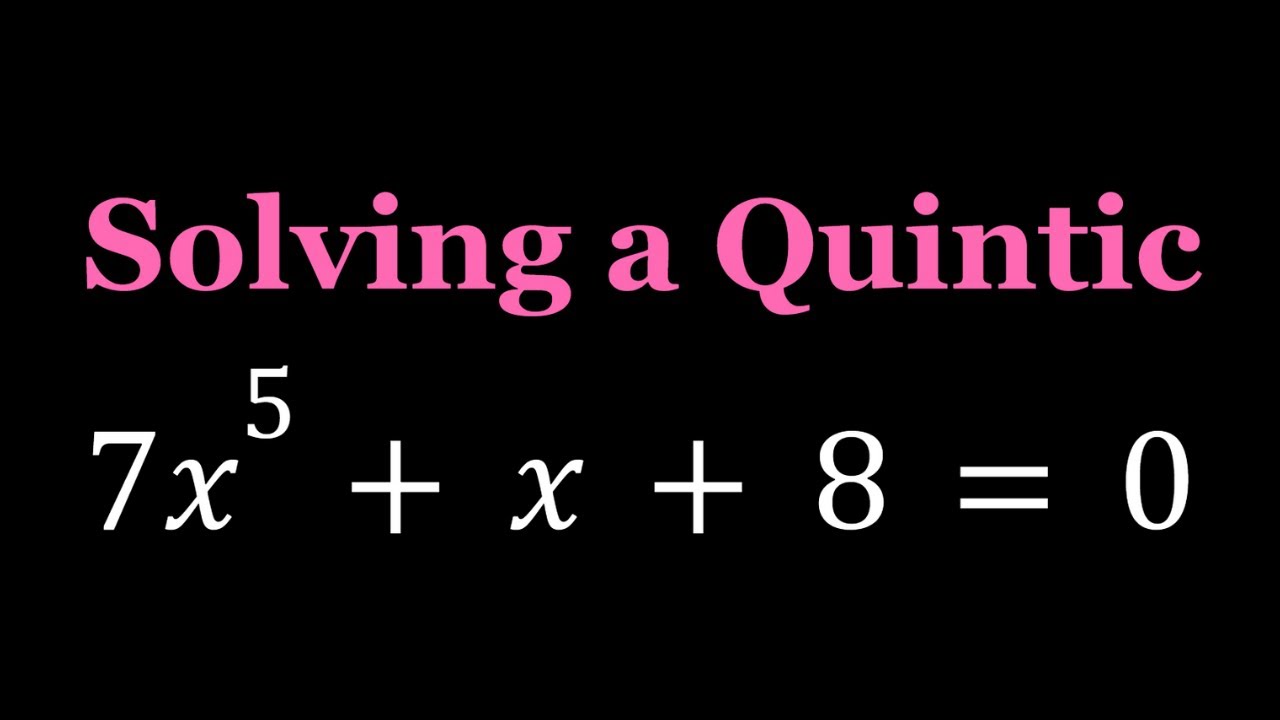
Показать описание
If you need to post a picture of your solution or idea:
#ChallengingMathProblems #PolynomialEquations
PLAYLISTS 🎵 :
#ChallengingMathProblems #PolynomialEquations
PLAYLISTS 🎵 :
Solving 7x^5+x+8 without Using the Quintic Formula
Linear equation with one unknown: Solve 5x=7x-8 step-by-step solution
Solve 7x-5=6x+8: Linear Equation Video Solution | Tiger Algebra
Solving an equation with variables on both side and one solution
[Bite-Size Guide] Solving Linear Equation “7𝑥 – 5 = 13𝑥 + 7” | Step-by-Step Algebra - Math Doodle...
[Bite-Size Guide] Solving Linear Equation “7𝑥 + 5 = 6𝑥 + 2” | Step-by-Step Algebra - Math Doodle...
Linear equation with one unknown: Solve 5x+8x-7x=5+1 step-by-step solution
Solve the following inequations : 7 x-5/8 x+34
Linear equation with one unknown: Solve 5x-8+7x-4=180 step-by-step solution
Linear equation with one unknown: Solve -(7x-8)=2-5x step-by-step solution
Simplify and Solve an Algebra Equation: 7x + 8 + 2x - 5 = 3x + 10 + 2x - 27
Algebra Shortcut Trick - how to solve equations instantly (2)
How to Solve Linear Equations in One Variable - Finding the Solution of an Equation
Linear equation with one unknown: Solve 5x+8-7x=-4x+1 step-by-step solution
Solving Linear Equations in One Variable - Grade 7 Math @MathTeacherGon
Solve -7x-5x+8=-16: Linear Equation Video Solution | Tiger Algebra
Solving Linear Equation “7𝑥 + 8 = –13” | Step-by-Step Algebra Solution - Math Doodle
Linear equation with one unknown: Solve 5/7x+4=8 step-by-step solution
Solving an equation for y and x
Solve Two Step Equation: 7x - 8 = 27
Solve x + 7 - 8x / 3 = 17 / 6 - 5x /8
Solve by completing the square | Step by Step Technique
Solve 3x + 7 = 5x - 23
Solve 7x-(5x+8)=8x-50: Linear Equation Video Solution | Tiger Algebra
Комментарии
 0:08:14
0:08:14
 0:01:21
0:01:21
 0:01:08
0:01:08
 0:02:36
0:02:36
![[Bite-Size Guide] Solving](https://i.ytimg.com/vi/hKKdpvN1tm8/hqdefault.jpg) 0:01:33
0:01:33
![[Bite-Size Guide] Solving](https://i.ytimg.com/vi/Z2G_P1jILj0/hqdefault.jpg) 0:01:21
0:01:21
 0:00:48
0:00:48
 0:07:20
0:07:20
 0:01:17
0:01:17
 0:01:49
0:01:49
 0:02:28
0:02:28
 0:05:33
0:05:33
 0:08:21
0:08:21
 0:01:32
0:01:32
 0:09:26
0:09:26
 0:01:22
0:01:22
 0:02:14
0:02:14
 0:01:17
0:01:17
 0:03:47
0:03:47
 0:01:33
0:01:33
 0:03:38
0:03:38
 0:05:20
0:05:20
 0:02:44
0:02:44
 0:01:54
0:01:54