filmov
tv
Finding tanα if tan(α+β)=7 and tan(α-β)=5
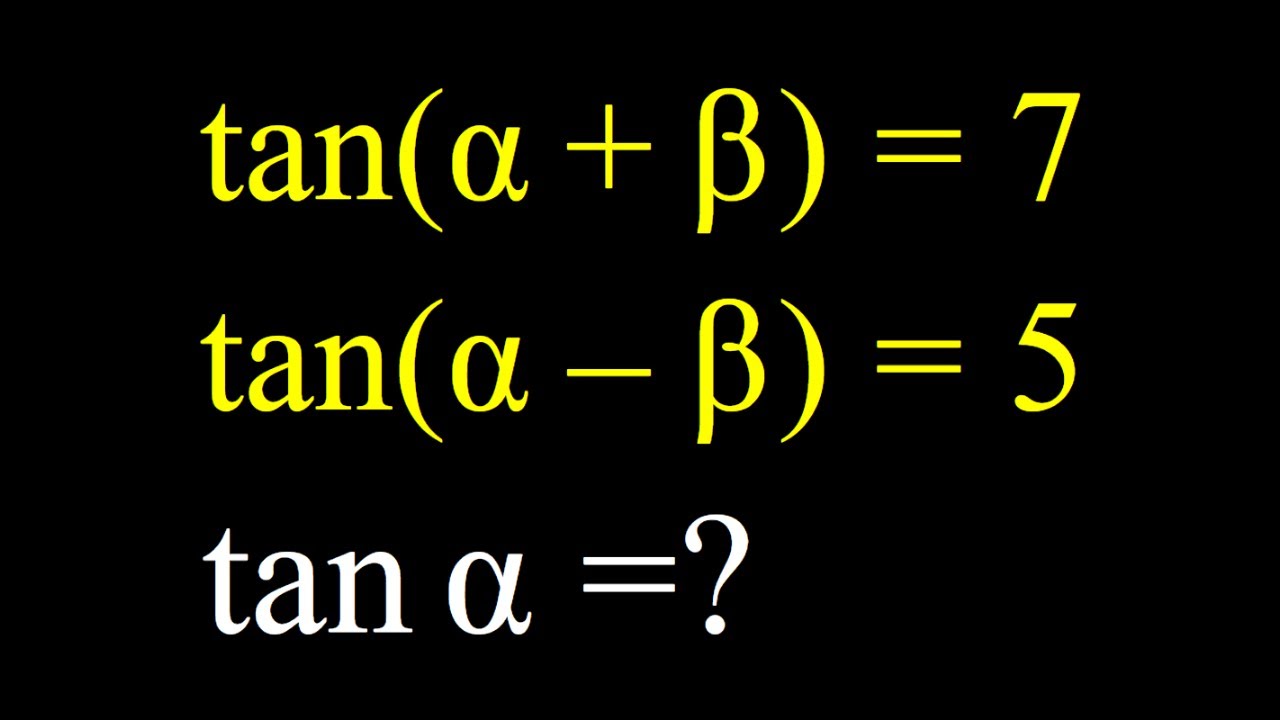
Показать описание
If you need to post a picture of your solution or idea:
#ChallengingMathProblems #TrigonometricExpressions
EXPLORE 😎:
PLAYLISTS 🎵 :
#ChallengingMathProblems #TrigonometricExpressions
EXPLORE 😎:
PLAYLISTS 🎵 :
Finding tanα if tan(α+β)=7 and tan(α-β)=5
tan(α-β)=?
How to prove the tangent compound angle identity tan(α - β) = [tan(α) - tan(β)] ÷ [1 + tan(α)tan(β)]...
Find tangent of the sum of 2 angles given info about alpha and beta
If tan alpha = 2/3, find sec x
AMBQID163 Question with Solution | Trigonometry | Find Tan Alpha Plus Beta | AMBPi83
And You Thought Trigonometry Was Pointless…
Sum or diff for sine or cosine give csc alpha and tan beta
7.2 5 - Sum Formula for Tangent
Given tanα=0.75,tanβ=2.4 find sin(α-β) Trigonometry Compound Angle
If tanβ=nsinαcosα/(1-n〖sin〗^2 α) , show that tan (α-β) = (1-n)tanα
Finding tan(A-B) part 1
tan a = 1/5 and tan b = 1/239 Find tan(4a - b) IMPORTANT
Scientist Modi Ji | Modi ji ka mathematics | Extra 2ab | Prem Sir
Chapter 10 Part - 8 | Proof: tan alpha + beta | 11 Class - P76
Find tan5, if tan19=a | trigonometry for 11th | Compound angles | Multiple angles | Math pagla |
Finding tanx when tan(2x-y)=3 and tan(y-x)=2
find the value of tan((alpha+beta))/2
Proving a Cool Trigonometric Identity
Finding tan(5) in terms of tan(19)
Heights and Distance Typical prob 2
A Fun Equation from Kettering University Math Olympiads
Double Angle Identities & Formulas of Sin, Cos & Tan - Trigonometry
Finding tan 65° when tan 35°=x in Two Ways
Комментарии
 0:12:37
0:12:37
 0:01:45
0:01:45
 0:02:01
0:02:01
 0:03:28
0:03:28
 0:00:37
0:00:37
 0:03:19
0:03:19
 0:01:00
0:01:00
 0:04:23
0:04:23
 0:08:27
0:08:27
 0:10:07
0:10:07
 0:03:46
0:03:46
 0:05:51
0:05:51
 0:05:52
0:05:52
 0:00:23
0:00:23
 0:03:32
0:03:32
 0:06:37
0:06:37
 0:10:19
0:10:19
 0:01:21
0:01:21
 0:10:30
0:10:30
 0:09:07
0:09:07
 0:05:19
0:05:19
 0:09:35
0:09:35
 0:18:16
0:18:16
 0:08:17
0:08:17