filmov
tv
Surjection from Evens to Natural Numbers | Injections and Surjections, Functions
Показать описание
In this lesson we prove the existence of a surjection from the even numbers to the natural numbers! Remember a surjective function from A to B is a function that covers B. As in, every element of B is getting mapped to by some element of A - or said another way: every element of B is the image of some element in A.
Proving this demonstrates that there are at least as many even numbers as there are natural numbers. Can you find an injective function from the evens to the naturals?
I hope you find this video helpful, and be sure to ask any questions down in the comments!
+WRATH OF MATH+
Follow Wrath of Math on...
Proving this demonstrates that there are at least as many even numbers as there are natural numbers. Can you find an injective function from the evens to the naturals?
I hope you find this video helpful, and be sure to ask any questions down in the comments!
+WRATH OF MATH+
Follow Wrath of Math on...
0:10:59
Surjection from Evens to Natural Numbers | Injections and Surjections, Functions
0:21:34
Bijection from Evens to Natural Numbers (With Proof!)
0:09:49
Bijective Functions and the Continuum Hypothesis
0:03:35
How to Prove a Function is Injective(one-to-one) Using the Definition
0:17:25
Functions, Domain, Codomain, Injective(one to one), Surjective(onto), Bijective Functions
0:06:32
2.1 - A Bijection between N and Z
0:07:40
Example: Making a Bijection
0:11:43
Bijections and Cardinality
0:05:44
Prove the Cardinality of the Integers is the same as the Cardinality of the Even Integers
0:07:39
Bijection between (0,1) and (-inf, inf)
0:10:02
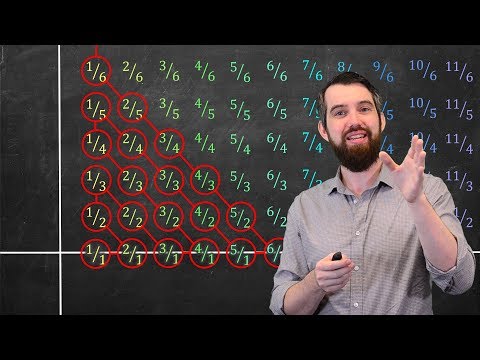
Countable and Uncountable Sets - Discrete Mathematics
0:07:14
Bijective Function Problem 1 - Functions - Discrete Mathematics
0:08:20
In each of the following cases, state whether function is one-one, onto or bijective f:R-R f(x)=3-4x
0:08:12
Class 12th – Bijective Function Numerical Example-2 | Relation and Functions | Tutorials Point
0:01:01
How do you determine if a function is a bijection from R to R?||Is 2x bijective?
1:25:07
Lecture 2: Cantor's Theory of Cardinality (Size)
0:08:05
A Hierarchy of Infinities | Infinite Series | PBS Digital Studios
0:38:35
Injective and Surjective Functions
0:08:42
(Abstract Algebra 1) Surjective Functions
0:10:22
Uncountability of the reals using their bijective correspondence with the subsets of natural numbers
0:12:38
Introduction To Surjective, Injective And Bijective Functions
0:03:38
Proving that a Set is Countable
0:08:51
Integers & Rationals are both infinite but is it the SAME infinity?
0:14:37
There is a bijection between Z+ and Z (Proof) [ILIEKMATHPHYSICS]
Комментарии