filmov
tv
Bijection between (0,1) and (-inf, inf)

Показать описание
Which interval contains more real numbers: (0, 1) or (-inf, inf)?
blackpenredpen,
math for fun
blackpenredpen,
math for fun
Bijection between (0,1) and (-inf, inf)
A bijection from (0,1) to (0,1] | Adding an element does NOT change the size of an infinite set!!
Define a bijection from [0, 1] to open interval (0, 1)
Explicit Bijection [0,1] to [0,1)
Mathematics: How to define a bijection between $(0,1)$ and $(0,1]$? (8 Solutions!!)
An unexpected bijection between the real plane and the real line
S01.9 Proof That a Set of Real Numbers is Uncountable
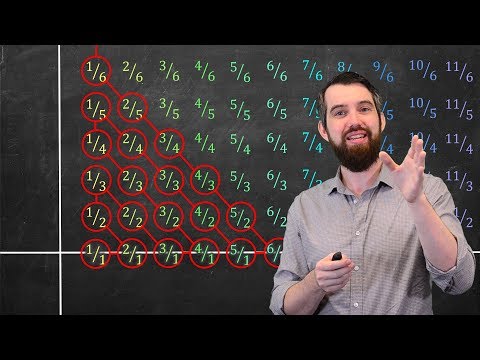
(0,1) is uncountable
Bijections and Cardinality
The Cardinality of an Interval
Is there a bijective map from $(0,1)$ to $mathbb{R}$? (10 Solutions!!)
WBCSC | Find an bijection from [0,1] to (0,1). KSA. Samir Sir
3.3.3 Counting with Bijections: Video
Mathematics: Is there a continuous bijective function $ f: [0,1) rightarrow Bbb R$? (3 Solutions!!)
Mathematics: On the existence of a continuous bijection $fcolon [0,1]to [0,1]times [0,1]$
my favorite 'which set has more elements' set theory problems
Example: Making a Bijection
(0,1) vs. the real numbers
2.1 - A Bijection between N and Z
Infinity Defied Counting Infinity Between 0 and 1
Bijective Function Problem 1 - Functions - Discrete Mathematics
Counting Infinity between 0 and 1 |Mark Zhuravlev Breakthrough Junior Challenge|
Integers & Rationals are both infinite but is it the SAME infinity?
Section 5.2-5.5, part 10 R2 and R have the same cardinality
Комментарии
 0:07:39
0:07:39
 0:02:54
0:02:54
 0:00:56
0:00:56
![Explicit Bijection [0,1]](https://i.ytimg.com/vi/0YnqO4E4cRU/hqdefault.jpg) 0:04:03
0:04:03
 0:04:49
0:04:49
 0:09:50
0:09:50
 0:04:02
0:04:02
 0:00:59
0:00:59
 0:11:43
0:11:43
 0:01:00
0:01:00
 0:05:21
0:05:21
 0:03:21
0:03:21
 0:11:43
0:11:43
 0:01:58
0:01:58
 0:02:30
0:02:30
 0:07:58
0:07:58
 0:07:40
0:07:40
 0:19:45
0:19:45
 0:06:32
0:06:32
 0:00:52
0:00:52
 0:07:14
0:07:14
 0:02:59
0:02:59
 0:08:51
0:08:51
 0:07:15
0:07:15