filmov
tv
Uncountability of the reals using their bijective correspondence with the subsets of natural numbers

Показать описание
In this video, using the famous Schroder-Bernstein Theorem, we show that there exists a bijective map from the power set of the set of natural numbers onto the set of real numbers. In the process we derive an alternative proof for the uncountability of the reals.
S01.9 Proof That a Set of Real Numbers is Uncountable
Episode 4: Uncountability of Real Numbers [#MathChops]
Real Analysis: Uncountability of reals using Nested Interval Theorem
The Set Of Real Numbers Is Uncountable
Real Analysis | The uncountability of ℝ
The Real Numbers. Uncountable.
An Alternative Proof That The Real Numbers Are Uncountable
The Real Numbers are Uncountable
The set of real numbers is uncountable (Proof) [ILIEKMATHPHYSICS]
MATH52: Lecture 30 - Uncountability of the Reals
6.3 Uncountability of the real numbers
Real Analysis Course #12 - (0,1) is Uncountable Using Diagonalization (Cantor Diagonalization)
Real Analysis-16: Set of Real Numbers is Uncountable (Via Nested Interval Property)
The Real Numbers are not listable/countable (Cantor's Diagonalisation Argument)
Real Numbers are Countable
prove that set r of real numbers is uncountable
Cantor's proof that the real numbers are uncountable
Set of Real Numbers is Uncountable Proof (by Cantor's Diagonal Argument)
Andrej Bauer: 'The countable reals'
Set of Real numbers is Uncountable | Cantor's diagonal argument | Discrete Mathematics
Uncountability of the reals using their bijective correspondence with the subsets of natural numbers
Reals are Uncountable
Reals are uncountable
Countability: The Real Numbers are Uncountable - Part 1
Комментарии
 0:04:02
0:04:02
 0:06:54
0:06:54
 0:10:13
0:10:13
 0:08:20
0:08:20
 0:08:18
0:08:18
 0:01:36
0:01:36
 0:07:20
0:07:20
 0:04:34
0:04:34
 0:10:04
0:10:04
 0:50:11
0:50:11
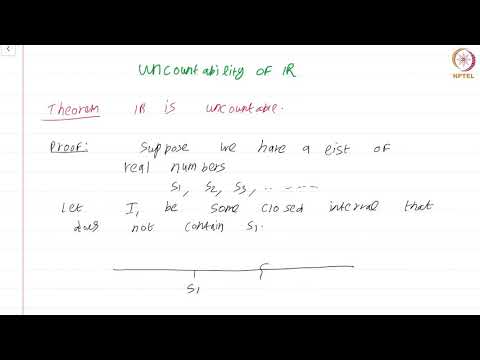 0:04:47
0:04:47
 0:05:24
0:05:24
 0:27:46
0:27:46
 0:12:23
0:12:23
 0:02:37
0:02:37
 0:00:57
0:00:57
 0:12:04
0:12:04
 0:04:44
0:04:44
 1:02:00
1:02:00
 0:06:59
0:06:59
 0:10:22
0:10:22
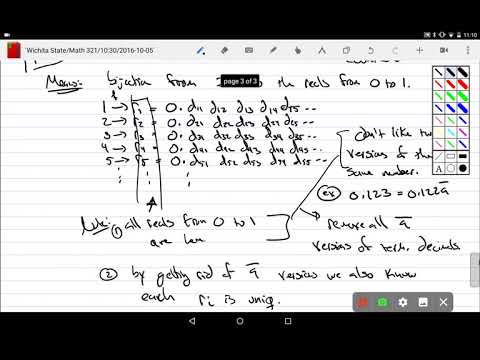 0:18:48
0:18:48
 0:09:28
0:09:28
 0:07:27
0:07:27