Countable and Uncountable Sets - Discrete Mathematics

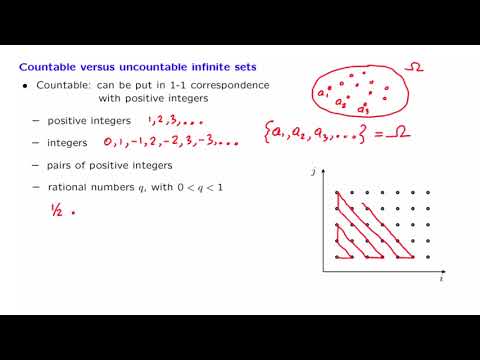
In this video we talk about countable and uncountable sets. We show that all even numbers and all fractions of squares are countable, then we show that all real numbers between 0 and 1 are uncountable.

Join this channel to get access to perks:

Hello, welcome to TheTrevTutor. I'm here to help you learn your college courses in an easy, efficient manner. If you like what you see, feel free to subscribe and follow me for updates. If you have any questions, leave them below. I try to answer as many questions as possible.

[Trevtutor]

It comes with video lectures, text lectures, practice problems, solutions, and a practice final exam!

[tjlavin]

I just realized this video in the DM1 series was recently posted. A massive thanks to you for continuing to update these playlists and get this guy in his 30s off to a great start in DM1 for a CS degree!!

[iiwvwjjfwwnevu]

I literally have an exam in 3 hours, and I couldn't find a video on countable sets from you last night but here you go, saving my life last minute

[Xennso]

I started learning this 3 days ago, im so glad you released a video on it! whenever I have problems understanding a discrete mathematics topic I instatly google the keyword and your name xD Thank you so much for content!

[Trevtutor]

I think this video is a bit overdue by now. But here we go: countable and uncountable sets!

[suyziljackson]

OMG. i was struggling to understand this concept and you explained it flawlessly!

[kaujla]

Thank you so much dude! Aside from the helpful content, the pacing of this video is perfect.

I've watched soo many other math, coding, etc. videos where they rush through the content or speak too quickly and it makes an otherwise informative video incredibly frustrating and worth disliking.

Glad I found your channel!

[Flaystray]

Wouldn't the uncountablity proof work for the natural numbers, too?

[gackerman]

afaik in this playlist we haven't yet talked about bijections/surjections etc. so this was a bit abrupt.

[Nino-eoey]

For the example shown at 2:07, if we keep the 0, can I set the function to be f(n) = 1/(n+1)²? It sounds correct, but something feels off about it.

[JwalinBhatt]

Thank for the video and the proof, but I am a bit confused. Wouldnt this make the natural numbers uncountable as well?
Lets say I have
a1=1
a2=2
a3=3

Now I go through all and keep appending them.
so a4=123
When I get to a123, the new number would get 123 appended at the end and hence wouldnt be in the set.
What am I missing?

[johannesndjimba]

Can you help me with this?
11. (15 points) Draw an undirected graph with six nodes and nine edges. Label the nodes 1
through 6. Write down the formal 2-tuple describing your graph. What is the
lexicographically first maximal independent set of your graph? Is it a maximum independent
set? Explain why or provide a maximum independent set.

[kanty]

my exams is tomorrow thanks god, helped me

[olayinkaanifowose]

So is it not a contradiction that we generated a real number greater than 0, but less than 1 and claimed for it not to be in the set of real numbers less than 1 and greater than zero? Surely this should reflect that the method breaks down somewhere?

[arthurlbn]

R/Q = Irrationals. All point in this set are an acummlation point?

[Daisynbn]

I understand how to make the new number but I don't understand what is its purpose. To prove that although we make a new set from original set, the new set is still uncountable?

[tonywang]

Thank you for the nice tutorial. But I think that last prove of accountability is not intuitive to me. All what we are trying to do is to show that there there much more numbers in (0, 1) than natural number. Instead, suppose I have the following mapping f:

0.1 to 1
0.11 to 2
0.111 to 3
...

Hences the number of 1s will map exactly to their corresponding natural number. lt obvious that all my input is from (0, 1), and the image is indeed natural number.

So now 0.2 is definitely a new number and it is in (0, 1), to include 0.2 into the domain of f, f(0.2) has to be one of the natural number that is already mapped, thus breaking the injective part of the bijective assumption.

[Flaystray]

2:18 why are you able to exclude zero?

[RFsalman]

2:10 isn't it because 0 is not in the natural number set ?

[johnpasses]

2:12
Sorry
Is zero in the set of natural numbers?