filmov
tv
The best step-by-step guide for factoring with the AC method and grouping
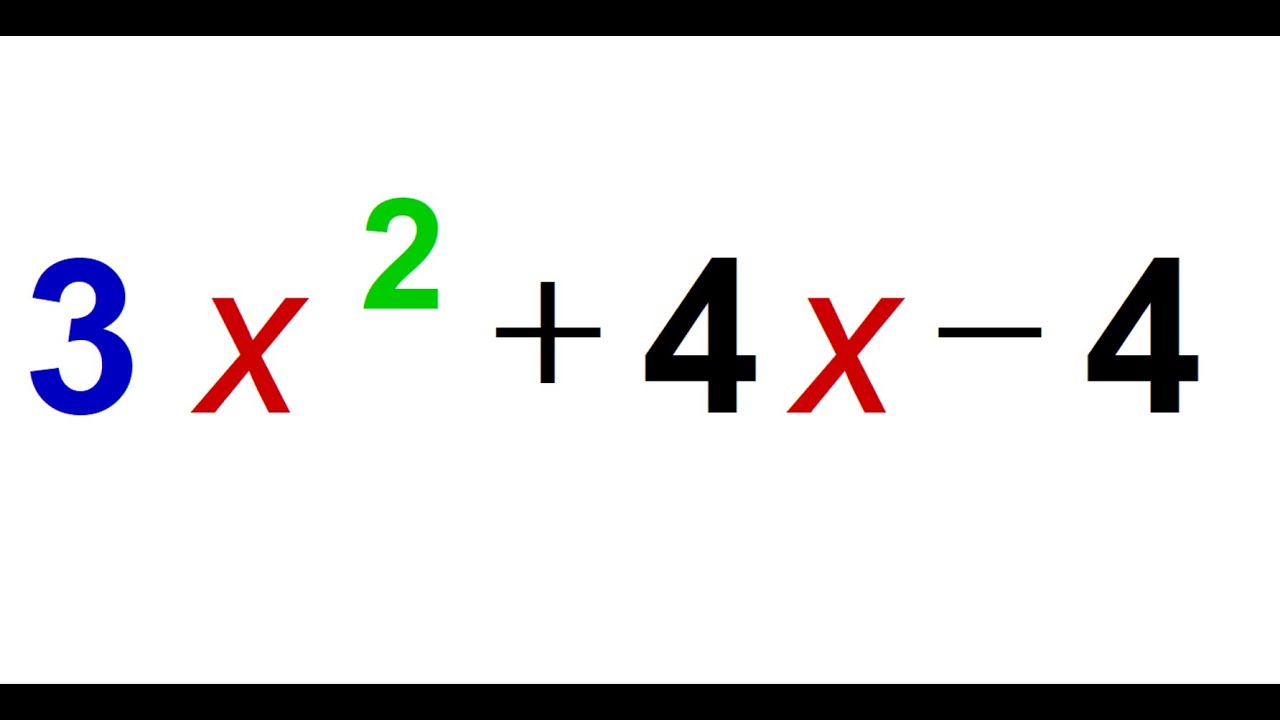
Показать описание
Title The Best Step-by-Step Guide for Factoring with the AC Method and Grouping 🤓✏️📚
Description
Welcome to the Math Magic Show 🎩✨, where we'll explore factoring a trinomial using the AC method and grouping! In this video, we'll break down the process of factoring an expression like 3x^2 + 4x - 4 step by step.
First, we identify the A and C values (3 and -4), then multiply them to get -12. This value helps us rewrite the middle term, 4x, using two numbers that multiply to -12 (our AC value) and add up to 4.
In this example, we find the numbers to be -2 and 6. We then rewrite the middle term as -2x + 6x, and use grouping to factor the expression. After some trial and error, we arrange the terms as 3x( x + 2) - 2(x + 2). Finally, we factor out the common term (x + 2) and arrive at our factored expression (3x - 2)(x + 2).
Join us on this math adventure to master the AC method and grouping in factoring trinomials! 🚀🧠🏆
Keywords
Common Internet Questions
1. How do I factor a trinomial using the AC method and grouping?
2. What are the steps in factoring trinomials?
3. How do I find the A and C values in a trinomial?
4. How can I rewrite the middle term of a trinomial using the AC method?
5. How do I use grouping to factor a trinomial?
6. Why is factoring trinomials important in algebra?
7. Can the AC method be used for all trinomials?
8. What is the easiest way to factor a trinomial?
9. How do I find the common factors in a trinomial?
10. Are there any tricks for factoring trinomials faster?
Description
Welcome to the Math Magic Show 🎩✨, where we'll explore factoring a trinomial using the AC method and grouping! In this video, we'll break down the process of factoring an expression like 3x^2 + 4x - 4 step by step.
First, we identify the A and C values (3 and -4), then multiply them to get -12. This value helps us rewrite the middle term, 4x, using two numbers that multiply to -12 (our AC value) and add up to 4.
In this example, we find the numbers to be -2 and 6. We then rewrite the middle term as -2x + 6x, and use grouping to factor the expression. After some trial and error, we arrange the terms as 3x( x + 2) - 2(x + 2). Finally, we factor out the common term (x + 2) and arrive at our factored expression (3x - 2)(x + 2).
Join us on this math adventure to master the AC method and grouping in factoring trinomials! 🚀🧠🏆
Keywords
Common Internet Questions
1. How do I factor a trinomial using the AC method and grouping?
2. What are the steps in factoring trinomials?
3. How do I find the A and C values in a trinomial?
4. How can I rewrite the middle term of a trinomial using the AC method?
5. How do I use grouping to factor a trinomial?
6. Why is factoring trinomials important in algebra?
7. Can the AC method be used for all trinomials?
8. What is the easiest way to factor a trinomial?
9. How do I find the common factors in a trinomial?
10. Are there any tricks for factoring trinomials faster?
 0:08:53
0:08:53
 0:10:45
0:10:45
 0:05:35
0:05:35
 0:57:53
0:57:53
 0:00:43
0:00:43
 0:01:07
0:01:07
 0:03:11
0:03:11
 0:10:24
0:10:24
 0:02:23
0:02:23
 0:19:23
0:19:23
 0:15:13
0:15:13
 0:10:27
0:10:27
 0:24:15
0:24:15
 0:11:35
0:11:35
 0:14:27
0:14:27
 0:07:29
0:07:29
 0:01:01
0:01:01
 0:06:53
0:06:53
 0:01:00
0:01:00
 0:42:08
0:42:08
 0:38:43
0:38:43
 0:33:49
0:33:49
 0:03:04
0:03:04
 0:13:36
0:13:36