filmov
tv
A Tricky Exponential Equation e^(x)=ln(x) | Lambert W Function | Math Olympiad
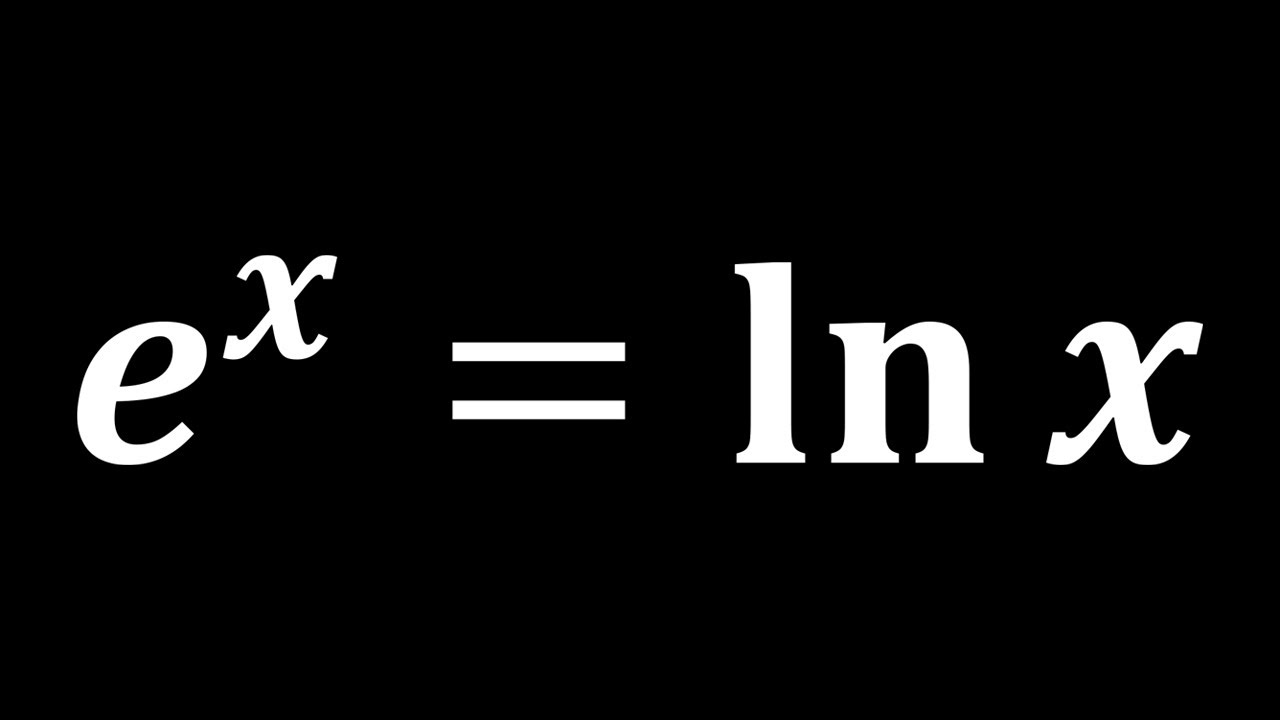
Показать описание
In this math algebra video, we shall solve a very nice exponential equation e^(x)=ln(x) by applying the rules of exponents, natural logarithms, and the lambert W Function. This question was taken from Mathematics Olympiad.
A Tricky Exponential Equation e^(x)=ln(x) | Lambert W Function | Math Olympiad
Solving Exponential Equations
How to solve the exponential equation x^ln(x)=2 by using logarithm
How do you solve an exponential equation with e as the base
Human Calculator Solves World’s Longest Math Problem #shorts
Exponential Equations - Algebra and Precalculus
How REAL Men Integrate Functions
AQA Core 3 1.03 Solving equations with e^x and ln(x)
Revision | Weeks 11 and 12
Solving an natural logarithmic equation using properties of logs
5 simple unsolvable equations
Solving x^{1/ln(x)}=e^{x-1}
Solving e^x=ln(x)/log(x)
When mathematicians get bored (ep1)
Solve for x, e^(3x +1) = k, and ln x + ln(x-1) = 1. Natural exponential equations
A Nice Exponential Equation e^x=x^e
Solving Exponential Equation
How do I find x? Exponential equation with two different bases. Reddit precalculus r/Homworkhelp
Solve the Exponential Equation e^2x = e^x + 6 using a u-sub
A Nice Exponential Equation with Ln(x)
Solving equations with ln x and e to the power x
How to solve this unbelievable exponential equation
How To Solve Exponential Equation x^5=9^x || Solving Exponential Equations.
Exponential Equations With Powers of X
Комментарии
 0:05:30
0:05:30
 0:16:36
0:16:36
 0:02:34
0:02:34
 0:02:47
0:02:47
 0:00:34
0:00:34
 0:05:58
0:05:58
 0:00:35
0:00:35
 0:10:30
0:10:30
 2:44:30
2:44:30
 0:01:15
0:01:15
 0:00:50
0:00:50
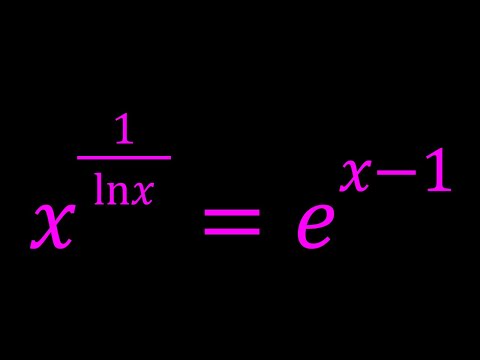 0:08:35
0:08:35
 0:06:25
0:06:25
 0:00:37
0:00:37
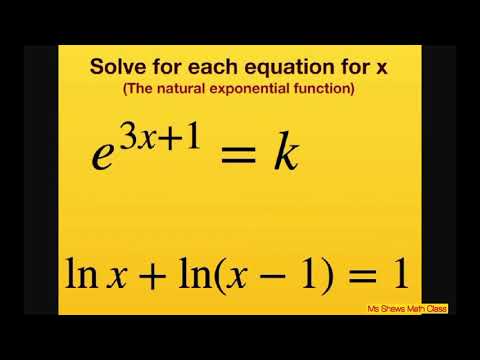 0:03:25
0:03:25
 0:09:59
0:09:59
 0:00:56
0:00:56
 0:07:47
0:07:47
 0:02:23
0:02:23
 0:08:52
0:08:52
 0:01:51
0:01:51
 0:03:20
0:03:20
 0:11:56
0:11:56
 0:05:22
0:05:22