filmov
tv
Solving e^x=ln(x)/log(x)

Показать описание
If you need to post a picture of your solution or idea:
#ChallengingMathProblems #ExponentialEquations
PLAYLISTS 🎵 :
#ChallengingMathProblems #ExponentialEquations
PLAYLISTS 🎵 :
Solving e^x=ln(x)/log(x)
Is e^x=ln(x) solvable?
Solving an natural logarithmic equation using properties of logs
Solving the Logarithmic Equation 5*ln(x) = 10
The Exponential Function e and The Natural Log ln
Natural Logarithms
What is e and ln(x)? (Euler's Number and The Natural Logarithm)
Solving Logarithmic Equations
Algebra 2 Regents Review (June 2024) #33-37 | Learning with Haneen #algebra
solving log(ln(x))=1 vs log(x)ln(x)=1, precalculus tutorial
Logarithms... How? (NancyPi)
ln(e^x)=x proof Learn How?
Simplify each natural exponential expression. Ln(ln e^(e^10), e^(x + ln x), e^(-2 ln 5)
e^x=ln(x)
Why does e^(ln x) = x
Solving Exponential Equation
Solving log(lnx)=ln(logx)
Relationship between Log(x) and Ln(x)
NATURAL LOGARITHM: SOLVING FOR X
What does LN(x) = in math?
Solving Logarithmic Equations... How? (NancyPi)
How do you solve an exponential equation with e as the base
Solving a natural logarithmic equation
AQA Core 3 1.03 Solving equations with e^x and ln(x)
Комментарии
 0:06:25
0:06:25
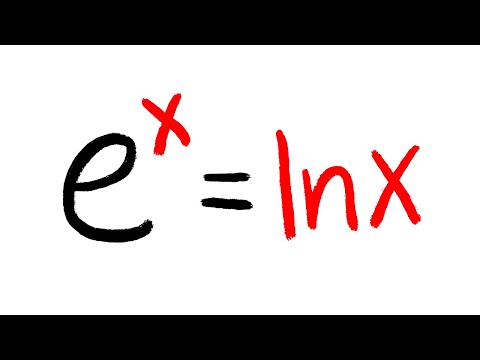 0:06:32
0:06:32
 0:01:15
0:01:15
 0:00:36
0:00:36
 0:10:16
0:10:16
 0:02:49
0:02:49
 0:12:02
0:12:02
 0:25:27
0:25:27
 0:30:20
0:30:20
 0:04:13
0:04:13
 0:19:15
0:19:15
 0:01:47
0:01:47
 0:04:41
0:04:41
 0:04:55
0:04:55
 0:02:05
0:02:05
 0:00:56
0:00:56
 0:08:35
0:08:35
 0:01:18
0:01:18
 0:04:41
0:04:41
 0:12:03
0:12:03
 0:15:05
0:15:05
 0:02:47
0:02:47
 0:03:07
0:03:07
 0:10:30
0:10:30